I teoremi di l'Hôpital
Si tratta di due tra i più famosi teoremi del calcolo infinitesimale, continuamente utilizzati (spesso anche a sproposito) per il calcolo dei limiti. É ormai quasi certo che questi teoremi, che portano il nome del marchese Guillaume F.A. de l'Hôpital, siano in realtà dovuti a Jean Bernoulli. Quest'ultimo (probabilmente a corto di soldi dopo il matrimonio) stipulò infatti un regolare contratto con il marchese in base al quale, dietro compenso di un regolare salario, si impegnava a comunicargli tutte le sue scoperte, lasciandogli la libertà di farne l'uso che desiderava. Il teorema fu pubblicato nel primo manuale di calcolo differenziale della storia: l'Analyse des infiniment petits del 1696. Una curiosità: Jean Bernoulli fa parte di una delle famiglie più prolifiche, sotto l'aspetto dei contributi alla fisica e alla matematica, della storia: almeno una dozzina di suoi membri si affermarono in una di queste discipline.
Enunciato dei teoremi
I due teoremi possono essere compendiati in un unico enunciato, come segue:
-
Regola di l'Hôpital per il
caso
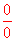 . Sia, in aggiunta
alle ipotesi precedenti,
. Sia, in aggiunta
alle ipotesi precedenti, 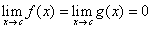 . Allora se
. Allora se 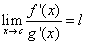 (eventualmente
anche ±∞) si ha anche
(eventualmente
anche ±∞) si ha anche 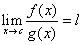 .
.
-
Regola di l'Hôpital per il
caso
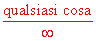 . Sia, in aggiunta
alle ipotesi precedenti,
. Sia, in aggiunta
alle ipotesi precedenti, 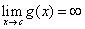 . Allora se
. Allora se 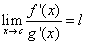 (eventualmente
anche ±∞) si ha anche
(eventualmente
anche ±∞) si ha anche 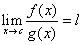 .
.
Osservazioni molto importanti
- Si noti che nel primo teorema entrambe le funzioni tendono a zero, nel secondo basta che il denominatore tenda all'infinito. In ogni caso l'applicazione più comune del secondo teorema è proprio al caso ∞/∞, tanto che nella maggior parte dei testi il teorema è enunciato in questo caso particolare e non in quello più generale da noi considerato.
- Questi teoremi sono largamente utilizzati per il calcolo di limiti nelle forme indeterminate, ma è necessaria un'applicazione non meccanica o maldestra che può allontanare dalla meta anziché aiutare a raggiungerla. Si noti anche che il teorema è applicabile solo ed esclusivamente nelle forme 0/0 e ∞/∞: le altre forme vanno ricondotte a queste. Si noti infine che in entrambi i casi si deve fare il limite del rapporto delle derivate, non della derivata del rapporto, che è tutta un'altra minestra.
-
Questi teoremi esprimono una condizione solo
sufficiente, ma non
necessaria per l'esistenza del limite del
rapporto di due funzioni: Può succedere che esista il
limite del rapporto delle funzioni senza che esista quello
delle derivate. Basta per esempio osservare che
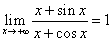 , mentre
, mentre 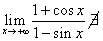 .
.
-
Questo teorema richiede la conoscenza delle derivate delle
funzioni in esame ed è per questo che il limite
fondamentale
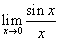 viene calcolato con
l'apposito noto teorema e non con il
teorema di l'Hôpital, che darebbe un risultato
immediato: per applicare la regola di l'Hôpital
bisogna saper fare la derivata della funzione seno e per
saper fare la derivata della funzione seno bisogna
già conoscere questo limite...
viene calcolato con
l'apposito noto teorema e non con il
teorema di l'Hôpital, che darebbe un risultato
immediato: per applicare la regola di l'Hôpital
bisogna saper fare la derivata della funzione seno e per
saper fare la derivata della funzione seno bisogna
già conoscere questo limite...
Esempi
Esempio 1. Calcolare ![]() .
Esso si presenta nella forma indeterminata ∞·0. Se
però lo riscriviamo come
.
Esso si presenta nella forma indeterminata ∞·0. Se
però lo riscriviamo come 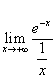 ,
si presenta nella forma 0/0. Calcolando il rapporto delle
derivate si ottiene il limite:
,
si presenta nella forma 0/0. Calcolando il rapporto delle
derivate si ottiene il limite: 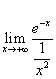 ,
che è ancora nella forma 0/0. Se si calcola nuovamente il
rapporto delle derivate si ottiene
,
che è ancora nella forma 0/0. Se si calcola nuovamente il
rapporto delle derivate si ottiene 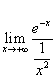 e
si vede subito che le cose vanno sempre peggio. Se si scrive
invece il limite come
e
si vede subito che le cose vanno sempre peggio. Se si scrive
invece il limite come ![]() , si ottiene la forma
∞/∞ e calcolando il rapporto delle derivate ci si
riduce al limite
, si ottiene la forma
∞/∞ e calcolando il rapporto delle derivate ci si
riduce al limite ![]() , che ha come risultato 0.
Prestare dunque la massima attenzione nel mutare la forma
∞·0 in 0/0 o in ∞/∞.
, che ha come risultato 0.
Prestare dunque la massima attenzione nel mutare la forma
∞·0 in 0/0 o in ∞/∞.
Esempio 2. Calcolare 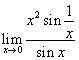 .
Poiché si ha la forma 0/0, calcolando il rapporto delle
derivate si ottiene
.
Poiché si ha la forma 0/0, calcolando il rapporto delle
derivate si ottiene 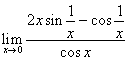 , e questo limite non
esiste. Si conclude che il teorema non è applicabile e
che il limite va calcolato per altra via. Si può operare
trasformando il limite in
, e questo limite non
esiste. Si conclude che il teorema non è applicabile e
che il limite va calcolato per altra via. Si può operare
trasformando il limite in ![]() che ha, banalmente,
valore 0.
che ha, banalmente,
valore 0.
Esempio 3. Calcolare ![]() .
Si presenta la forma indeterminata 0/0. calcolando il rapporto
delle derivate si vede subito che la situazione peggiora e non
si riesce a concludere. Operando la sostituzione 1/x=t
il limite si può scrivere nella forma
.
Si presenta la forma indeterminata 0/0. calcolando il rapporto
delle derivate si vede subito che la situazione peggiora e non
si riesce a concludere. Operando la sostituzione 1/x=t
il limite si può scrivere nella forma ![]() .
Una sola applicazione della, ormai famosa, regola produce il
risultato: 0.
.
Una sola applicazione della, ormai famosa, regola produce il
risultato: 0.
Esempio 4. Calcolare il ![]() . Poiché si ha la forma ∞/∞, se si
calcola il rapporto delle derivate si ottiene
. Poiché si ha la forma ∞/∞, se si
calcola il rapporto delle derivate si ottiene ![]() e non si cava un ragno dal buco. Il limite si calcola
invece banalmente con un procedimento standard:
e non si cava un ragno dal buco. Il limite si calcola
invece banalmente con un procedimento standard: 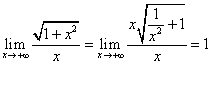 . Si osservi che, a -∞, si avrebbe invece
. Si osservi che, a -∞, si avrebbe invece 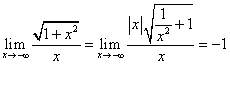 .
.
Esempio 5. Si considerino le due funzioni f(x)=1+x+cosxsinx e g(x)=esinx(x+sinxcos x). Si supponga di dover calcolare il limite del loro rapporto per x tendente a +∞. Non è difficile provare che sia f che g tendono a +∞, mentre il rapporto f/g non ha limite. Il rapporto delle derivate ha invece (non è difficile da provare) limite zero. Dunque il limite del rapporto delle derivate esiste, mentre il limite del rapporto delle funzioni non esiste. Il motivo è da ricercarsi nel fatto che la derivata di g si annulla infinite volte in un intorno di +∞, mentre una delle condizioni per la validità del teorema è proprio il non annullarsi della derivata del denominatore.
Alcuni limiti notevoli
Utilizzando la regola di l'Hôpital si possono facilmente dimostrare alcuni limiti notevoli in maniera molto agevole (una loro dimostrazione per altra via sarebbe possibile ma tecnicamente molto più complicata). Li raggruppiamo qui, invitando il lettore a dimostrarli per esercizio.
-
Per ogni a>0 e per ogni b si ha
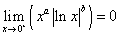 .
.
-
Per ogni a>0 si ha
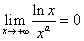 .
.
-
Per ogni a si ha
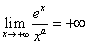 .
.