Introduzione
Consideriamo un polinomio di primo grado: f(x)=ax+b che ha come grafico una retta nel piano cartesiano. Questa funzione gode di una proprietà fondamentale: se, a partire da un dato punto c incrementiamo di un certo tratto Δx la variabile indipendente, la variabile dipendente risulterà incrementata di un tratto Δy, proporzionale a Δx secondo la costante a. La verifica è immediata: Δy = f(c+Δx) - f(c) = a(c+Δx)+b - (ac+b) = aΔx.
Se consideriamo una retta passante per l'origine, f(x)=ax, allora esiste proporzionalità addirittura tra le variabili indipendente e dipendente, e non solo tra gli incrementi delle variabili. Le rette passanti per l'origine sono un esempio molto semplice (ma molto importante) di funzioni lineari tra spazi vettoriali, funzioni che giocano un ruolo cruciale nell'algebra lineare. (Sull'algebra lineare puoi consultare una monografia, nella sezione inglese di questo sito).
Se consideriamo una funzione più complessa tale proporzionalità non esiste più. Prendiamo ad esempio in esame la funzione f(x)=x2 e consideriamo il punto c=1. Valutando gli incrementi Δy in corrispondenza ad incrementi Δx via via decrescenti possiamo controllare nella tabella qui sotto che non esiste proporzionalità, ma che comunque il rapporto Δy/Δx si avvicina al valore 2, man mano che Δx decresce: per piccolissimi valori di Δx potremo ritenere Δy e Δx sostanzialmente proporzionali. Ciò significa che nelle immediate vicinanze del punto c=1, il legame tra gli incrementi delle variabili potrà essere considerato di proporzionalità diretta, esattamente come se la funzione fosse una retta: in altre parole potremo approssimare la funzione di secondo grado con una retta, di cui 2 sarà il coefficiente angolare. Poiché tale retta deve passare per lo stesso punto (1,1) per cui passa la funzione f(x)=x2, la sua equazione sarà: y=2x-1.
| Δx | Δy | Δy/Δx |
| 100 | 10200 | 102 |
| 10 | 120 | 12 |
| 1 | 3 | 3 |
| 0.1 | 0.2100000000 | 2.1 |
| 0.01 | 0.0201000000 | 2.01 |
| 0.001 | 0.0020010000 | 2.001 |
| 0.0001 | 0.0002000100 | 2.0001 |
| 0.00001 | 0.0000200001 | 2.00001 |
| 0.000001 | 0.0000020000 | 2.000001 |
| 0.0000001 | 0.0000002000 | 2.0000001 |
Osserviamo che la retta y=2x, parallela alla precedente e passante per l'origine, è proprio la funzione che stabilisce il legame approssimato tra Δx e Δy che emerge, per piccolissimi valori di Δx, dalla tabella riportata sopra: Δy=2Δx. Questa retta si chiamerà differenziale della funzione data (in questo caso f(x)=x2) nel punto1 e sarà indicata con la notazione dfx=1 o, brevemente, df1: df1(x)=2x.
In sostanza il differenziale di una funzione f in un punto c è, quando esiste, una retta r passante per l'origine che permette di calcolare in maniera approssimata gli incrementi Δy in funzione di Δx, per Δx molto piccoli.
Esaminiamo ora la stessa tabella da un altro punto di vista: il rapporto tra Δy e Δx, per ogni fissato valore di Δx, rappresenta il coefficiente angolare della retta passante per i punti P=(1 , f(1))=(1,1) e Q=(1+Δx , f(1+Δx)), retta che potremo chiamare secante la curva, in analogia a quello che si fa con la circonferenza. Se consideriamo valori di Δx sempre più piccoli, i punti P e Q sul grafico della funzione diventano sempre più vicini, fino a coincidere: potremo dire, ancora in analogia con la circonferenza, che la retta secante tende a diventare tangente alla curva, e che il rapporto tra Δy e Δx tende a diventare proprio il coefficiente angolare della tangente. Questo rapporto limite è detto derivata della funzione f nel punto 1 ed è indicato con la scrittura f'(1). Poiché il coefficiente angolare della tangente può essere determinato anche con metodi elementari di geometria analitica, sarà facile controllare la coerenza di questo calcolo.
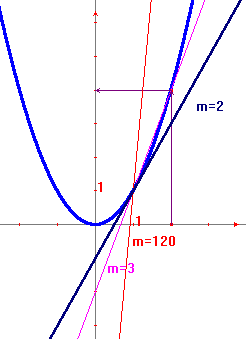
Riesaminando la precedente definizione di differenziale, potremo concludere che la derivata della funzione è il coefficiente angolare della retta che rappresenta il differenziale: dunque mentre la derivata è un numero, il differenziale è una funzione. I due concetti sono comunque sostanzialmente identici (una retta per l'origine è univocamente individuata dal suo coefficiente angolare) e, se ci limitiamo alle funzioni di una variabile, non vale la pena di fare troppo i sofisti: poiché è molto più facile maneggiare i numeri che non le funzioni, potremo tranquillamente limitarci a considerare solo le derivate. La questione cambia radicalmente quando si passa a considerare funzioni di più variabili. Chi è interessato ad approfondire il concetto di differenziale può consultare una monografia apposita in questo sito.
In sostanza il problema che è emerso dalle considerazioni intuitive più sopra riportate può essere sintetizzato come segue: data una funzione f di R in R, verificare se, in un intorno opportuno di un dato punto c, la funzione può essere approssimata con una retta, nel senso che gli incrementi della funzione possano essere valutati sulla retta anziché sul grafico della curva che rappresenta la funzione. Il problema può essere tecnicamente ricondotto a quello di determinare il coefficiente angolare di una retta che avrà tutte le caratteristiche per essere chiamata tangente al grafico della funzione.
La cosa interessante di tutto questo è che le tecniche introdotte per la soluzione di questo problema hanno aperto un intero nuovo capitolo della matematica, il cosiddetto Calcolo differenziale, che si è rivelato di fondamentale importanza in tutti i campi.
Anche in questo campo, come e forse più che in altri, l'avvento delle nuove tecnologie ha introdotto nuove e stimolanti prospettive didattiche: è ora possibile concentrarsi molto di più sulla sostanza del problema anziché sulle complicazioni tecniche e di calcolo. Siamo quindi assolutamente contrari a proporre esercizi inutilmente complicati e lunghi che possono contribuire a far rendere antipatico e noioso allo studente questo affascinante capitolo della matematica.
A proposito di questo argomento vi invitiamo a leggere lo splendido libretto dal titolo Matematici, di Giorgio Tomaso Bagni, ed. Antilia, Treviso 2000, di cui abbiamo riportato alcuni passi della prefazione.