Definizione 
Consideriamo una funzione 
cioè una
funzione a valori reali definita in un sottoinsieme D dei numeri
reali. Poiché ci interesseranno problemi connessi al
concetto di derivata e quindi di tangente, supporremo che D sia
un intervallo o un'unione di intervalli, e considereremo
solo punti interni.
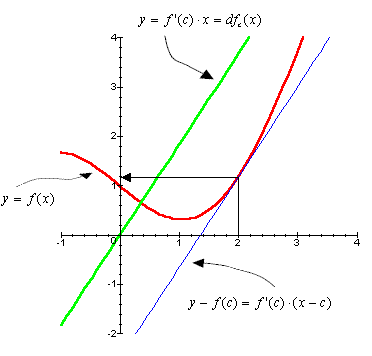
Sia c un punto dove la funzione f è derivabile. Allora la retta y-f(c) = f'(c)× (x-c) è tangente al grafico della funzione nel punto (c,f(c)). La funzione che ha come grafico la parallela a questa retta, passante per l'origine, cioè la retta y = f'(c)× x, è detta differenziale della funzione f nel punto c e si indica con dfc.
La definizione formale di
differenziale di una funzione in un punto c ove la funzione
è derivabile è dunque:
In base alla definizione data si vede che il differenziale esiste se e solo se esiste la derivata.
Nel grafico qui sotto è riportata una funzione f, la sua tangente in un punto e il differenziale della funzione nello stesso punto.
Consideriamo, come esempio, la funzione f(x) = x3-2x+3, e il punto di ascissa 1 del dominio. Poiché f(0) = 3 ed f'(0) = -2, l'equazione della retta tangente é y-3 = -2(x-1), cioè y = -2x+5, mentre il differenziale è la funzione df0(x) = -2x. In un punto generico, c, il differenziale sarà dato dalla regola: dfc(x)=(3c2-2)x. Si noti, in quest'ultima formula, che la variabile della funzione differenziale è x, non c. Sempre da quest'ultima formula risulta evidente che il differenziale della funzione f è una funzione che generalmente cambia da punto a punto, ma siccome ha sempre come grafico una retta passante per l'origine, l'unico cambiamento sarà nella pendenza.
