Ma a che serve? 
Per le funzioni che stiamo considerando (reali di una variabile reale) il differenziale è un concetto non molto importante, essenzialmente per il fatto che il differenziale di una funzione esiste se e solo se esiste la derivata. In sostanza il concetto di differenziale non porta nuovi contributi teorici sostanziali rispetto a quello di derivata. Ben diverso è il caso delle funzioni di più variabili, in cui il concetto di differenziale diventa essenziale. Le applicazioni di questo concetto sono però molto importanti anche nel caso di funzioni reali di una variabile reale e si basano sulle considerazioni che seguono.
Se consideriamo un punto c del dominio di una funzione
(dove la funzione è derivabile) e un punto c+h,
la quantità f(c+h)-f(c) si chiama incremento
della funzione relativo al punto c e all'incremento h, e si
indica con Δfc(h). La valutazione di
questo incremento è molto importante nelle applicazioni.
Questo incremento, come vedremo tra poco, è calcolabile,
con un'approssimazione da valutare, se si conosce il
differenziale della funzione f nel punto c. La formula
che interessa è: Δfc(h) 
dfc(h). Per rendersi conto di
questo fatto basta considerare il grafico qui sotto.
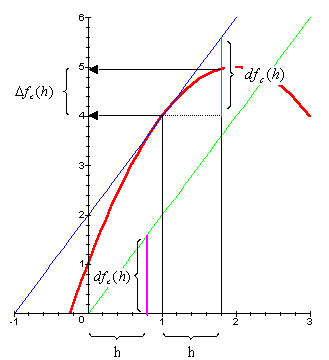
É ovvio che Δfc(h) e
dfc(h) sono diversi, ma è
altresì facilmente intuibile dal grafico che la
differenza tra queste due quantità è tanto
più piccola quanto più è piccolo
l'incremento h della variabile indipendente (basta per
questo osservare che la quantità
dfc(h), che va calcolata utilizzando il
grafico del differenziale -linea verde nella figura- è
uguale alla seconda quantità indicata con lo stesso
simbolo e colore fucsia nella figura).
Un filmato può evidenziare ancora meglio
quanto appena affermato.
Si usa indicare la differenza Δfc(h) - dfc(h) con E(h), errore che si commette approssimando l'incremento con il valore del differenziale. Si può provare che questa differenza, al tendere a zero di h, tende a zero molto più velocemente di h. É in questo senso che intendiamo dire che la prima quantità può essere approssimata con la seconda. Poiché, ovviamente, dfc(h) tende a zero al tendere a zero di h, tenendo conto di quanto appena dimostrato, nelle applicazioni si usa dire che dfc è una variazione infinitamente piccola della funzione, quando la variabile subisce una variazione infinitamente piccola.
Per fare questa verifica calcoliamo il limite del rapporto tra E(h) e h. Si ha:
.
E questo basta per dire che, se h è piccolo, E(h) è infinitamente più piccolo di h.
Se consideriamo ora la funzione f(x)=x (questa funzione si chiama funzione identità , perché ad ogni x fa corrispondere x stesso, e si può indicare con i: f(x)=i(x)), la sua derivata in un punto qualunque vale sempre 1, per cui il suo differenziale, in ogni punto, è sempre la funzione dic(x)=1·x=x, cioè la funzione i stessa, che è come dire dic=i. É invalsa l'abitudine di indicare la funzione i(x)=x semplicemente con il simbolo x, e siccome il differenziale di questa funzione non dipende dal punto c, si tralascia l'indicazione di c, per cui si usa scrivere di=dx=x.
Si tratta di un'abitudine che si applica a tutte le funzioni. Consideriamo alcuni esempi:
- Se f è la funzione x→ sin(x), f si chiama funzione sin(x), mentre si dovrebbe dire funzione sin.
- Se f è la funzione x→ x2, f si chiama funzione x2, mentre si dovrebbe dire funzione elevamento al quadrato.
- Se f è la funzione x→ex, f si chiama funzione ex, mentre si dovrebbe chiamare funzione esponenziale di base e.
La ragione di questa abitudine sta nel fatto che, generalmente, il nome che si dovrebbe usare per le funzioni è molto complesso. Per esempio nel caso, molto semplice, della funzione f: x→x2+x3, si dovrebbe dire somma tra la funzione elevamento al quadrato e la funzione elevamento al cubo, espressione prolissa che si preferisce sostituire con: funzione x2+x3. Bisogna comunque prestare attenzione a questo fatto per non commettere grossolani errori.
A questo punto se consideriamo una qualunque funzione derivabile
si può scrivere
dfc(x)=f'(c)·x=f'(c)·dx,
ovvero dfc=f'(c)·dx, che si usa
scrivere semplicemente df=f'·dx. Se
dx≠ 0 da qui si trae 
,
che si scrive:
Da
quest'ultima uguaglianza ha origine un modo di pensare alle
derivate che è diventato abituale, in particolare nelle
applicazioni: la derivata di una funzione
è il rapporto tra il differenziale della variabile
dipendente e quello della variabile indipendente
Se si tiene conto di quanto sopra detto relativamente al fatto che hanno interesse le variazioni "infinitesime" della variabile indipendente, si può ulteriormente affermare che:
La derivata di una funzione può essere considerata, a livello elementare, come il rapporto tra una variazione infinitesima della variabile dipendente e una variazione infinitesima della variabile indipendente.