Notazioni ed osservazioni
Intervalli di numeri reali e loro rappresentazione grafica
Tra i sottoinsiemi dell'insieme, R, dei numeri reali con la usuale struttura di corpo ordinato ci interesseranno in modo particolare gli intervalli. Se a e b sono due numeri reali, con a<b, adotteremo le seguenti definizioni, simbologie e rappresentazioni grafiche:
 Intervallo limitato aperto
|
]a,b[ |
{x 
R | a < x < b}
|
|
|
Intervallo limitato chiuso
|
[a,b] |
{x
R | a ≤ x ≤ b}
|
|
|
Intervallo limitato aperto a
destra
|
[a,b[ |
{x
R | a ≤ x < b}
|
|
|
Intervallo limitato aperto a
sinistra
|
]a,b] |
{x
R | a < x ≤ b}
|
|
|
Intervallo inferiormente illimitato
aperto
|
]-∞,a[ |
{x
R | x < a}
|
|
|
Intervallo inferiormente illimitato
chiuso
|
]-∞,a] |
{x
R | x ≤ a}
|
|
|
Intervallo superiormente illimitato
aperto
|
]a,+∞[ |
{x
R | a < x}
|
|
|
Intervallo superiormente illimitato
chiuso
|
[a,+∞[ |
{x
R | a ≤ x}
|
|
Poiché avremo a che fare quasi esclusivamente con
sottoinsiemi di R, di norma tralasceremo
l'indicazione x
R e le parentesi graffe e useremo le notazioni
semplificate: a < x < b, ecc.
I connettivi logici
Nello scrivere l'insieme delle soluzioni di una equazione o
disequazione è opportuno evitare l'uso delle
congiunzioni "e" ed "o", a
causa dei diversi significati che esse possono avere nella
lingua italiana. In genere è preferibile utilizzare i
connettivi logici 
ed 
("vel" ed "et"),
oppure i simboli della teoria degli insiemi 
ed
∩ ("unione" ed
"intersezione"). Per esempio per scrivere
l'insieme dei valori esterni all'intervallo di estremi 2
e 5, cioè l'insieme 
,
scriveremo x<2 x>5
oppure x<2 x>5.
A proposito però dei connettivi logici è comunque da tenere presente che un loro uso corretto è spesso difficile e, come in molte altre circostanze, è preferibile usare la logica del buon senso (M.Dolcher, Elementi di Analisi): i simboli logici vanno utilizzati quando c'è pericolo di confusione e si è assolutamente sicuri di averne capito il significato. Piuttosto che usarli a sproposito è meglio servirsi delle usuali espressioni della lingua italiana, magari rischiando di essere prolissi.
Giova qui puntualizzare anche il significato preciso della
scrittura a≥b: essa è equivalente a
a>b a=b. É per questo che
3≥3 è vera, in quanto equivale a 3>3 (falsa) 3=3 (vera).
Segno delle funzioni
Avremo bisogno di una opportuna rappresentazione grafica per studiare il segno delle funzioni di variabile reale. Le funzioni che considereremo sono, di norma, positive o negative su intervalli e si annullano su punti isolati. Anche il dominio naturale è di solito costituito dall'unione di un numero finito di intervalli. Per questi casi semplici utilizzeremo le seguenti convenzioni:
- _____________________ (linea continua). Indica gli intervalli dove la funzione è strettamente positiva.
- ------------------------- (linea tratteggiata). Indica gli intervalli dove la funzione è strettamente negativa.
- o (zero). Indica i punti, o gli intervalli, dove la funzione si annulla.
- ×. Indica i punti (o gli intervalli) dove la funzione non è definita.
Notazioni speciali, evidenti dal contesto, potranno essere usate in casi speciali. Anche qui, come a proposito dei connettivi logici, sarà opportuna una buona dose di "logica del buon senso".
Per chiarire il concetto segnaliamo che un grafico come quello qui sotto si riferisce ad una funzione che risulta:
-
Definita per x<-5
-5<x<12.
-
Strettamente positiva per x<-5
1≤x<3
3<x<8.
-
Strettamente negativa per -5<x<1
8<x<12.
-
Nulla per x=3 x=8.
Tavole di verità e tavole di segno.
Avremo spesso bisogno di considerare contemporaneamente più disequazioni (per fare l'unione o l'intersezione degli insiemi di soluzioni) o il segno di più funzioni (per trovare il segno del prodotto o del quoziente delle varie funzioni). Per agevolare la discussione rappresenteremo in un unico grafico i vari insiemi di soluzioni o i segni delle diverse funzioni, come negli esempi che seguono.
Esempio 1: determinazione delle soluzioni comuni a due
disequazioni. Se le due disequazioni hanno gli insiemi di
soluzioni indicate nel grafico qui sotto, è immediato
concludere che le soluzioni comuni si hanno negli
intervalli:
-2≤x<2
5≤x≤7 9<x<13.
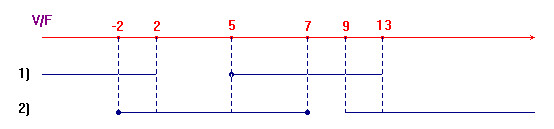
Si noti l'indicazione V/F che abbiamo posto in alto a sinistra per ricordare che il grafico in questo si riferisce ai "valori di verità" di due disequazioni. Un grafico come questo lo chiameremo una tavola di verità .
Esempio 2: determinazione del segno del prodotto di due
funzioni. Se due funzioni hanno i segni indicati nel
grafico qui sotto, è immediato concludere che il loro
prodotto è positivo per 2<x<5
8<x<13 x>16,
negativo per x<2
5<x<8 13<x<16, nullo per x=2 x=5 x=8 x=13
x=16.
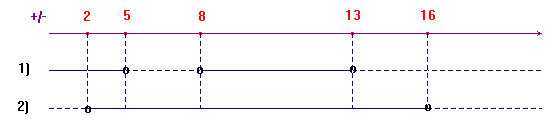
Si noti l'indicazione +/- che abbiamo posto in alto a sinistra del grafico per ricordare che questo grafico riporta il segno di una o più funzioni.
In entrambi i grafici l'unità di misura in orizzontale non ha alcun interesse, mentre è (ovviamente!) fondamentale l'ordine dei numeri (chiamati anche caposaldi).