Regole di calcolo con le disuguaglianze
R come corpo commutativo ordinato
Nel risolvere le disequazioni intervengono le proprietà della relazione d'ordine introdotta nei reali. Questa relazione (indicata con ≤, che si legge minore od uguale) è di ordine totale, cioè gode delle seguenti proprietà:
- Riflessiva. Per ogni reale x si ha x ≤ x.
-
Antisimmetrica. Se x ed y sono due
reali, allora da x ≤ y
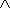y ≤ x segue x = y.
-
Transitiva. Se x, y, z
sono tre reali, allora da x ≤ y 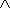y ≤ z segue x
≤ z.
-
Totalità dell'ordine. Se x ed
y sono due reali deve essere x ≤
y
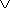y ≤ x (se sono
entrambe vere si deve necessariamente avere x =
y). Questo significa che due reali sono sempre
confrontabili.
Invece di scrivere x ≤ y si può anche scrivere, in maniera perfettamente equivalente, y ≥ x (y è maggiore od uguale ad x). Oltre a questa relazione si considera anche la relazione "<" definita da: x < y equivale a x ≤ y ed x ≠ y. In maniera analoga si definisce la relazione ">". Queste due relazioni non sono di ordine nel senso classico del termine (per esempio non sono riflessive).
É molto importante il fatto che questa relazione di ordine è compatibile con la struttura di corpo commutativo introdotta su R mediante le operazioni di addizione e moltiplicazione, o in altri termini, che R è un corpo commutativo ordinato. Ciò significa che valgono le seguenti due proprietà:
- Compatibilità dell'ordine con l'addizione. Se x, y, z sono tre reali e si ha x ≤ y, si ha anche x+z ≤ y+z. Questo dice che in una disuguaglianza si può sommare uno stesso numero ad ambo i membri, mantenendo la validità della disuguaglianza.
-
Compatibilità dell'ordine con la
moltiplicazione. Se x ed y sono due
reali e z è un reale strettamente positivo
(z>0), allora da x ≤ y si
deduce anche xz ≤ yz. Questo dice che in
una disuguaglianza si possono moltiplicare ambo i membri per
uno stesso numero maggiore di zero, mantenendo la
validità della disuguaglianza.
Se invece z<0 allora da x ≤ y segue xz ≥ yz. Questo dice che se in una disuguaglianza si moltiplicano ambo i membri per uno stesso numero minore di zero, allora bisogna cambiare il verso della disuguaglianza.
Queste due proprietà delle disuguaglianze sono alla base di tutte le manipolazioni algebriche che si eseguono per risolvere le disequazioni.
Disequazioni equivalenti
Due disequazioni si dicono equivalenti se hanno lo stesso insieme di soluzioni. La risoluzione delle disequazioni si basa principalmente sulla possibilità di ridurre una disequazione ad una, o più, disequazioni equivalenti, di cui siano noti i metodi risolutivi. Per fare questo si usano le due proprietà di compatibilità sopra elencate. Poiché però le disequazioni coinvolgono una (o due) incognite sono opportune alcune precisazioni.
Sia data la
disequazione f(x) > g(x), e sia D il suo
dominio. É possibile sommare ad ambo i membri della
disequazione (per ottenere una disequazione equivalente) una
stessa funzione h(x), che abbia ancora dominio
D.
-
Esempio 1. Le disequazioni
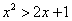e 
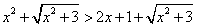sono equivalenti perché
l'aggiunta della radice non ha modificato il dominio (che
è R).
-
Esempio 2. Le disequazioni
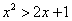e
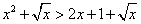non sono equivalenti,
perché l'aggiunta della radice ha eliminato dal
dominio i reali negativi.
-
Esempio3. Le disequazioni
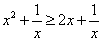e 
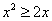(la seconda è
stata ottenuta dalla prima sommando -1/x e semplificando) non
sono equivalenti, perché hanno diverso dominio. Per
renderle equivalenti dovrei mantenere l'informazione
x≠0 contenuta nella prima e non nella seconda, per esempio
scrivendo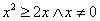 
.
Sia data la
disequazione f(x) > g(x), e sia D il suo
dominio. É possibile moltiplicare ambo i membri della
disequazione (per ottenere una disequazione equivalente) per una
stessa funzione h(x) strettamente positiva
purché abbia ancora dominio D.
-
Esempio 1. Le disequazioni
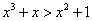e 
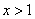sono equivalenti perché la
seconda è stata ottenuta dalla prima moltiplicando per
1/(x2+1) che non altera il dominio ed
è strettamente positiva.
-
Esempio 2. Le disequazioni
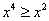e 
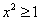non sono equivalenti perché
la seconda è stata ottenuta dalla prima moltiplicando
per 1/x2, che non comprende lo zero nel
dominio.
Dalle proprietà di compatibilità discendono facilmente anche le seguenti, di frequente uso:
Due disequazioni dello stesso
verso e con lo stesso dominio possono sempre essere sommate
membro a membro.
Due
disequazioni dello stesso verso e con lo stesso dominio
non possono essere moltiplicate membro a
membro, a meno che tutti i membri non siano
strettamente positivi.
Ne segue che di norma non si possono elevare ambo i membri di una disequazione al quadrato (o ad una potenza pari), a meno che i due membri non siano positivi, mentre si possono sempre elevare ad una potenza dispari. Per esempio da -2<1 non segue 4<1 (elevando al quadrato), mentre segue -8<1 (elevando al cubo).