Il binomio di primo grado f(x)=ax+b
Una disequazione di primo grado si può sempre porre in una delle forme:
- ax + b > 0
- ax + b < 0
- ax + b ≥ 0
- ax + b ≤ 0
con a e b reali e a ≠ 0. Graficamente il primo membro è rappresentato da una retta nel piano cartesiano, dove a è il coefficiente angolare e b l'ordinata all'origine. La rappresentazione grafica rende immediata la soluzione della disequazione, una volta trovata (equazione di primo grado!) l'intersezione della retta con l'asse delle ascisse (la retta non può essere parallela all'asse delle ascisse perché si è supposto a ≠ 0).
Risoluzione grafica
La disequazione 2x + 5 > 0, per esempio, si risolve
immediatamente osservando il grafico qui sotto, ottenendo come
insieme delle soluzioni la semiretta 
.
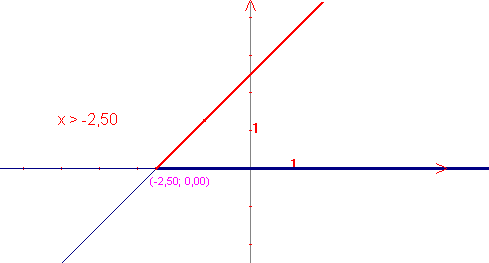
Lo stesso grafico fornisce immediatamente le opportune conclusioni riguardo il segno del binomio 2x + 5: esso è positivo per x>-2.5, negativo per x<-2.5, si annulla per x=-2.5. Secondo le convenzioni adottate, rappresentiamo questi risultati graficamente nel seguente modo:
-
Soluzioni della disequazione 2x + 5 > 0:
-
Segno del binomio 2x + 5:
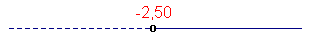
Puoi vedere un'animazione con CabriJava relativa a questo tipo di disequazioni.
Risoluzione algebrica
La risoluzione della disequazione può naturalmente avvenire per pura via algebrica, applicando le proprietà delle disuguaglianze. Da ax+ b > 0 si passa ad ax > -b, dopodiché si divide ambo i membri per a (facendo attenzione al suo segno) e si conclude immediatamente. Anche se in questo caso la risoluzione algebrica è più veloce di quella grafica, è comunque opportuno abituarsi a maneggiare con disinvoltura la tecnica grafica, che diventerà essenziale in seguito.
Esempi
-
: 
-
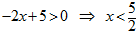sgn(-2x+5) :
-
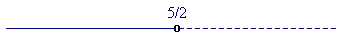
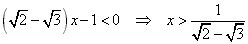(si noti che il coefficiente di
x è negativo!).
Osservazione importante
Si noti che nel risolvere le disequazioni di primo grado (o nel trovare il segno di un binomio di primo grado) la determinazione del dominio non è importante, perché sempre coincidente con R. In casi più complessi ricordarsi di trovare sempre prima il dominio naturale.