Operazioni tra funzioni-2
Tra tutte le possibili operazioni tra funzioni consideriamo alcuni casi particolari, frequenti nelle applicazioni.
Il passaggio al reciproco
Si tratta, data una funzione f(x), di ottenere il grafico della funzione 1/f(x). Si può osservare che in tutti gli intervalli ove f(x) cresce, il suo reciproco decresce, e viceversa. Per una trattazione significativa è opportuno anche fare qualche considerazione, seppure a livello intuitivo, su alcuni limiti. In particolare ci interessano le seguenti osservazioni:
- Nei punti in cui f(x) vale zero, il reciproco non è definito e tende all'infinito (quindi con presenza di asintoti verticali).
- Nei pressi dei punti dove f(x) tende all'infinito, il reciproco tende a zero.
Come al solito proporremo alcuni esempi per chiarire il metodo da seguire.
Esempi
| f(x)=x2-x-2 | f(x)=1/(x2-x-2) |
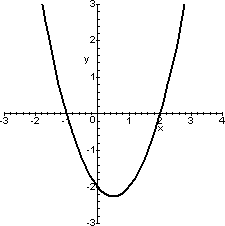
|
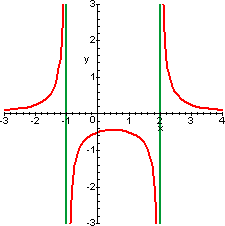
|
| f(x)=lnx | f(x)=1/lnx |
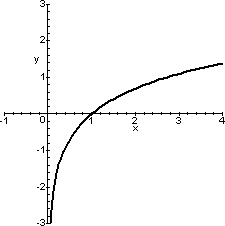
|
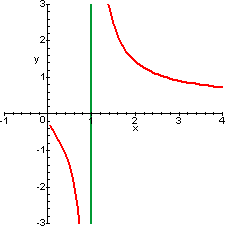
|
Da f(x) a ln(f(x))
Poiché la funzione logaritmo naturale è strettamente crescente nel suo dominio, data una funzione f(x), la funzione ln(f(x)) sarà crescente o decrescente esattamente come f(x). Naturalmente occorrerà tenere conto che ln(f(x)) è definita solo dove f è positiva. Per una trattazione significativa è opportuno anche fare qualche considerazione, seppure a livello intuitivo, su alcuni limiti. In particolare ci interessano le seguenti osservazioni:
- Nei punti in cui f(x) vale zero, il ln(f(x)) non è definito e tende a meno infinito (dal lato ove f è positiva), quindi con presenza di asintoti verticali.
- Nei pressi dei punti dove f(x) tende a più infinito, anche ln(f(x)) tende a più infinito.
Nel caso di logaritmi in altre basi, basterà solo ricordare che se la base è maggiore di uno, il logaritmo è crescente (e quindi si comporta come il logaritmo naturale), mentre se la base è compresa tra zero ed uno il logaritmo è decrescente. Come al solito proporremo un esempio per chiarire il metodo da seguire.
| f(x)=x2-x-2 | f(x)=ln(x2-x-2) |
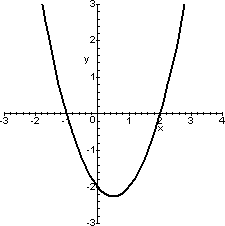
|
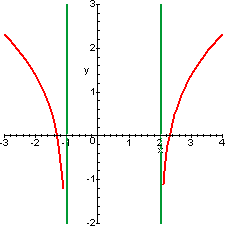
|
Da f(x) a ef(x)
Poiché la funzione esponenziale è strettamente crescente, data una funzione f(x), la funzione ef(x) sarà crescente o decrescente esattamente come f(x). Naturalmente occorre ricordare che ef(x)è sempre positiva. Per una trattazione significativa è opportuno anche fare qualche considerazione, seppure a livello intuitivo, su alcuni limiti. In particolare ci interessano le seguenti osservazioni:
- Nei pressi dei punti ove f(x) tende a meno infinito, ef(x) tende a zero.
- Nei pressi dei punti dove f(x) tende a più infinito, anche ef(x) tende a più infinito.
Come al solito proporremo un esempio per chiarire il metodo da seguire.
| f(x)=1/(x2-x-2) |
|
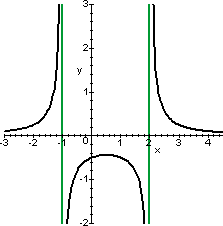
|
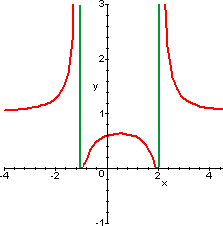
|
Considerazioni analoghe si possono fare per passare da f(x) a √(f(x)).