Alcune sostituzioni importanti 
La ricerca delle primitive di alcune funzioni può essere ricondotta a quella di una funzione razionale con opportune sostituzioni. Ne esamineremo alcune, senza alcuna pretesa di completezza. In questa pagina indicheremo con r(x) una funzione razionale nella variabile reale x.
Le funzioni r(x) che
contengono un radicale, di indice m, di un polinomio di
primo grado 
possono essere ricondotte
all'integrazione di una funzione razionale fratta mediante
la sostituzione 
. Per esempio per calcolare
, se si pone 
, ci si ritrova con l'integrale 
, che si calcola facilmente. Stessa tecnica se il
radicando è un quoziente di due polinomi di primo grado
Le funzioni r(x) che
contengono un radicale del tipo 
si possono ricondurre all'integrazione di funzioni
razionali fratte secondo una delle due sostituzioni seguenti:
-
se a>0, ponendo
;
-
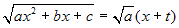se a<0 il polinomio deve necessariamente avere
due radici per avere valori reali; indicandole con α e
β (α<β) basterà osservare che
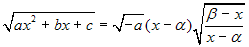, per ricondursi al caso di un radicale
con un quoziente di polinomi di primo grado.
Per esempio per calcolare 
, se si pone 
, e si trova 
; ci si riconduce all'integrale, immediato,
.
Le funzioni r(ex)
ed r(tgx) possono essere integrate come funzioni
razionali con la sostituzione ex=t oppure
tgx=t.
Le funzioni razionali in sinx
e cosx possono essere integrate come funzioni razionali
con la sostituzione 
e ricordando le
cosiddette formule parametriche: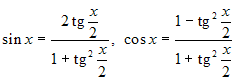 
.
Esistono numerose altre sostituzioni standard che possono ricondurre il calcolo di una primitiva ad un altra, spesso di funzione razionale fratta, ma non riteniamo opportuno insistere ulteriormente su questo argomento: come già detto nessun insieme, per quanto ampio, di strategie può risolvere il problema di calcolare le primitive delle funzioni elementari, e anche le tecniche presentate in questa pagina hanno più che altro lo scopo di confermare le difficoltà di questo problema, piuttosto che quello di fornire un elenco esaustivo.