Funzioni razionali fratte 
L'integrazione delle funzioni razionali fratte occupa un capitolo a sé nel del calcolo delle primitive, innanzitutto per la sua grande importanza nelle applicazioni e poi perché dal punto di vista tecnico il problema può essere ricondotto a quello della ricerca degli zeri di un polinomio. In sostanza le primitive di una funzione razionale fratta possono essere determinate con una tecnica standard se si riesce a decomporre in fattori il polinomio al denominatore.
Le primitive fondamentali
Cominciamo a calcolare le primitive di tre tipi fondamentali di
funzioni razionali fratte, a cui tutti gli altri si possono
ricondurre: 
-
.
-
.
-
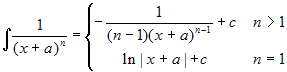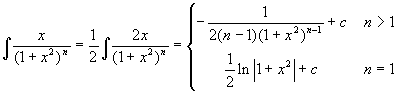Se n=1 l'integrale è immediato:
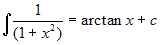. Per n >1 si può usare una
formula ricorrente. Posto 
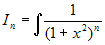, si trova : 
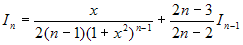. Mediante questa formula, applicata
quante volte serve, il calcolo di In
è ricondotto a quello, noto, di
I1.
Ci servirà poi saper ricondurre a questi il calcolo
seguente: 
. Si tratta di eseguire
alcune manipolazioni algebriche e una
sostituzione opportuna .
Decomposizione in fratti semplici
Consideriamo una generica funzione razionale fratta; si possono presentare due situazioni:
- il grado del numeratore è maggiore od uguale a quello del denominatore;
- il grado del numeratore è minore di quello del denominatore.
Nel primo caso si può eseguire la divisione tra
numeratore e denominatore, ottenendo: 
(Q è il quoziente e R è il
resto). La frazione "residua" è del tipo
"2". La ricerca delle primitive di N/D si
riconduce dunque alla ricerca di quelle di R/D, in
quanto Q è un polinomio. Basta dunque
considerare il secondo caso. Per esse vale il seguente
, con N e D polinomi primi fra di loro,
la frazione si può sempre decomporre in una somma finita
di frazioni del tipo 
e 
, con 
. Precisamente:
-
Ogni radice reale a del denominatore, di
molteplicità p, contribuisce alla predetta
somma con i seguenti p addendi:
.
-
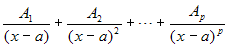Ogni radice complessa α+iβ del denominatore, di
molteplicità q assieme alla sua coniugata
α-iβ, contribuisce alla predetta somma con i
seguenti q addendi:
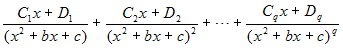, ove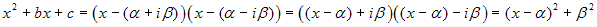 
.
Questo teorema consente di ricondurre il calcolo delle primitive di una qualunque funzione razionale fratta a quella degli integrali fondamentali proposti sopra. Esso permette, tenendo conto degli integrali fondamentali considerati sopra, di concludere che
Le
primitive di una funzione razionale fratta sono sempre
costituite da una combinazione lineare finita di funzioni
razionali (anche intere), e funzioni del tipo 
oppure 
.
Esempi
Calcolare 
. Si ha 
. Se si riduce
quest'ultima somma di frazioni allo stesso denominatore, si
trova un numeratore di terzo grado, con coefficienti dipendenti
da A, B, C, D. Questo
numeratore deve essere uguale al numeratore del primo membro:
per il principio di identità dei polinomi si
troverà un sistema lineare di quattro equazioni in
quattro incognite, che ci permetterà di trovare i quattro
coefficienti incogniti A, B, C,
D. Si ottiene: A=1, B=1,
C=-1, D=0. I primi due addendi si integrano
facilmente, per l'ultimo si opera come segue: 
. Si deve ulteriormente modificare il secondo addendo tra
parentesi, come segue: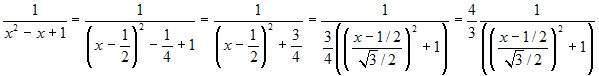 
.
Basterà ora porre 
, cioè 
, da cui 
. Riunendo tutti i risultati ottenuti si
trova, infine, 
.
Calcolare 
. Si ha 
. Con il metodo sopra
indicato si trova A=-1, B=-1, C=1. Si
ha subito: 
.