La funzione exp(-1/x2)
La funzione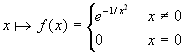 
ha un comportamento molto
interessante per quanto riguarda il problema della
approssimazione con polinomi. Non è difficile provare,
infatti, che essa è indefinitamente derivabile e che
tutte le sue derivate sono nulle nell'origine. Questo
significa che il suo polinomio di Taylor, di punto iniziale 0,
è il polinomio nullo, indipendentemente dall'ordine
voluto. In altri termini questo significa che l'unica
approssimazione accettabile della funzione con un polinomio, in
un intorno dell'origine, è quella con il polinomio
nullo, cioè con la retta tangente.
Questa particolarità della funzione considerata ci
consente di costruire altri esempi interessanti. Sia data, per
esempio, la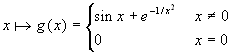 
. E' immediato che il
suo polinomio di Taylor, di ordine n=2k+1,
coincide con quello della funzione seno: 
.
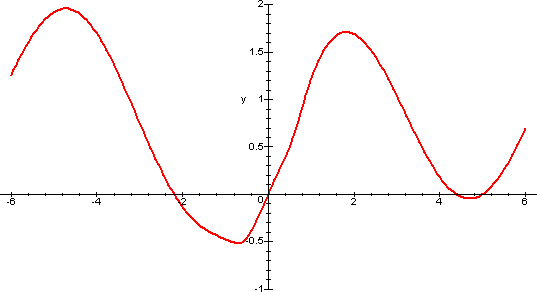
Utilizzando i link sottostanti puoi visualizzare la funzione g(x) (in rosso) e i polinomi approssimanti di diverso ordine (in blu), verificando che, all'aumentare del grado del polinomio, il grafico si "adagia" sempre meglio e su un intervallo sempre più grande sul grafico della funzione sin(x), che non coincide affatto con quello di g(x): l'aumento del grado del polinomio non modifica la bontà dell'approssimazione già fornita dalla tangente.
|
|
|
|
|
|
|
| uno | due | tre | quattro | cinque | sei | sette |
