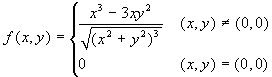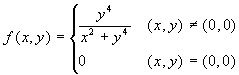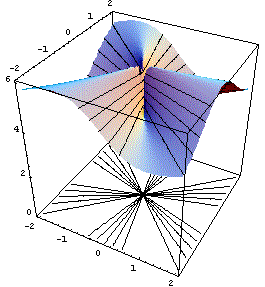
Non ha limite nell'origine: le curve di livello sono semirette per l'origine, situate a quote diverse.

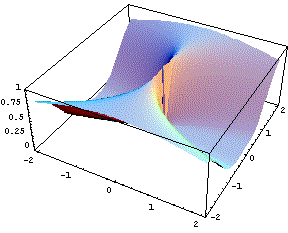
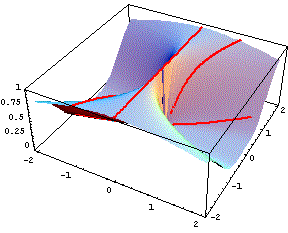
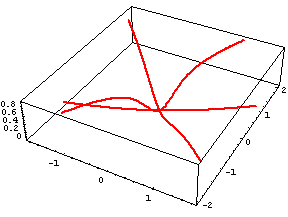
Non ha limite nell'origine. Le due figure qui sotto illustrano il fatto che le curve sezione della superficie con un piano verticale per l'origine tendono tutte a 0 al tendere di (x,y) a (0,0), tranne quella ottenuta per sezione con x=0, che vale costantemente 1.

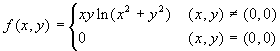
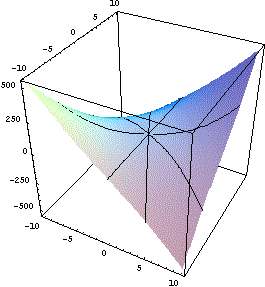
Questa volta tutte le curve ottenute per sezione con un piano verticale per l'origine passano per z=0. Ma ciò non basterebbe per concludere che il limite della funzione è zero. Se però si esegue una trasformazione in coordinate polari si trova: , da cui si può concludere che il limite vale zero.