Indagini sulla continuità - 4
Vogliamo ora esaminare su un esempio che cosa succede se
calcoliamo un limite in due variabili mediante due limiti
successivi, facendo prima tendere la x al valore
prefissato e poi la y. Per fare questo consideriamo la
funzione 
, il cui è grafico è
rappresentato qui sotto.
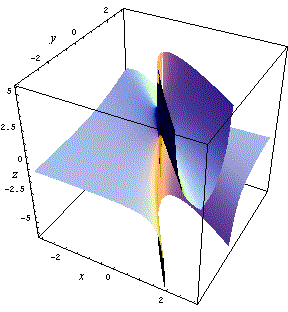
Consideriamo per esempio il problema del calcolo del limite per (x,y) tendente a (0,0), dove la funzione non è definita e dove si annullano sia il numeratore che il denominatore della frazione.
Scegliamo un punto (x,y), nei pressi di zero e, tenendo
fisso y (che supponiamo diverso da zero e da uno),
facciamo tendere x a zero. Così facendo il punto
(x,y,z)=(x,y,f(x,y)) sulla superficie
tenderà ad un punto del piano x=0, appartenente
alla curva intersezione della superficie con questo piano. Il
calcolo è molto semplice e dà: 
. Ora facciamo tendere y a zero: il punto
(x,y,z) si muoverà lungo la predetta curva
intersezione e si ottiene 
. Simmetricamente
supponiamo di tenere fisso x e facciamo tendere
y a zero: il punto (x,y,z) si muoverà
sulla superficie tendendo ad un punto della curva appartenente
all'intersezione tra la superficie e il piano y=0.
Anche ora il calcolo è semplice e si ottiene 
. Da qui segue subito che 
. I
due limiti sono diversi. La funzione in due variabili non
può avere limite. Nelle figure qui sotto sono
rappresentate le due curve intersezione tra i piani
x=0, o y=0 con la superficie.
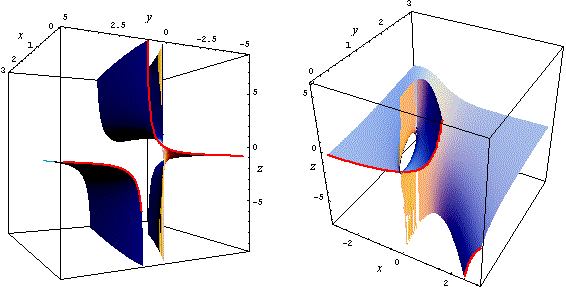
Il problema è naturalmente legato al fatto che i percorsi per raggiungere il punto (0,0) a partire dal generico punto (x,y) sono diversi e, come già osservato negli esempi precedenti, in generale il limite di una funzione di due variabili può dipendere dal percorso scelto: solo se il limite "globale" in due variabili esiste, allora la traiettoria seguita è indifferente.
La tecnica di calcolare il limite su particolari restrizioni in genere serve a provare che un determinato limite non esiste: basta provare che su due restrizioni diverse si ottengono limiti diversi. Se invece su restrizioni diverse si ottengono limiti uguali, in genere nulla si può affermare sull'esistenza del limite; l'unica conclusione che si può trarre è sull'eventuale valore del limite stesso: se, in qualche modo, si riesce a provare che il limite esiste, allora deve necessariamente essere uguale a quello calcolato su una qualunque restrizione.