Esercizi su continuità e derivabilità - 2
Esercizio 1 Si dica per quali valori
di α>0 e β>1 la funzione 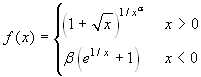 è prolungabile per continuità in zero. La funzione
prolungata è derivabile? Per la prima parte si tratta di
fare i limiti per x tendente a zero, da destra e da
sinistra. Si ha:
è prolungabile per continuità in zero. La funzione
prolungata è derivabile? Per la prima parte si tratta di
fare i limiti per x tendente a zero, da destra e da
sinistra. Si ha: 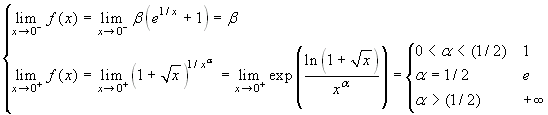 . Per il calcolo del
secondo limite abbiamo tenuto conto che
. Per il calcolo del
secondo limite abbiamo tenuto conto che 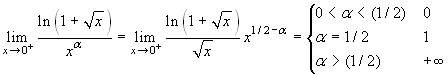 .
Possiamo concludere, tenendo conto che deve essere β>1,
che la funzione è prolungabile per continuità se e
solo se α=1/2 e β=e.
.
Possiamo concludere, tenendo conto che deve essere β>1,
che la funzione è prolungabile per continuità se e
solo se α=1/2 e β=e.
Per controllare la derivabilità in 0 della funzione così prolungata dobbiamo fare il limite del rapporto incrementale sinistro e destro. Si potrebbe anche fare la derivata per gli x negativi e per quelli positivi e poi fare il limite delle due derivate (vedi il Teorema sul limite della derivata), con, sostanzialmente, le stesse difficoltà di calcolo. Si ottiene:
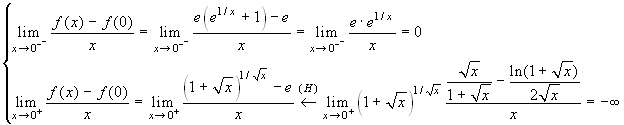
Pertanto la funzione non è derivabile.
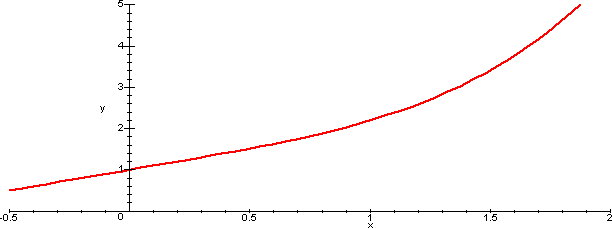
Può essere utile visualizzare il grafico della funzione per i valori di α e β che la rendono continua anche in 0.
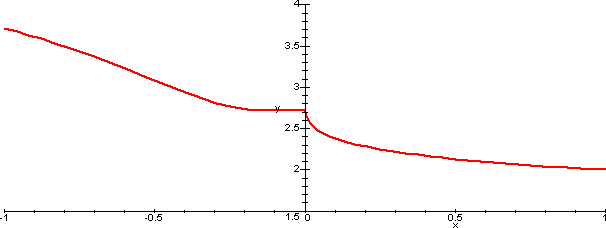
Esercizio 2 Dati α, β,
γ, δ, si consideri la funzione 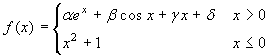 . Per
ogni k≥0 si dica per quali valori di α,
β, γ, δ la funzione è di classe
Ck(R) (continua con le sue
derivate fino all'ordine k). La funzione è
chiaramente continua e derivabile indefinitamente su tutto
R, tranne che per x=0, dove richiede
un'analisi specifica. Ne calcoliamo le derivate successive
per x≠0.
. Per
ogni k≥0 si dica per quali valori di α,
β, γ, δ la funzione è di classe
Ck(R) (continua con le sue
derivate fino all'ordine k). La funzione è
chiaramente continua e derivabile indefinitamente su tutto
R, tranne che per x=0, dove richiede
un'analisi specifica. Ne calcoliamo le derivate successive
per x≠0.
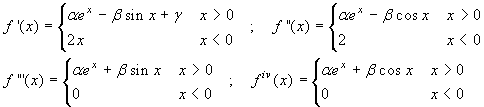
Facendo i limiti sinistro e destro in zero della funzione e delle sue derivate si conclude che:
- la funzione è di classe C0(R) se α + β + δ = 1;
- la funzione è di classe C1(R) se α + γ = 0;
- la funzione è di classe C2(R) se α - β = 2;
- la funzione è di classe C3(R) se α = 0.
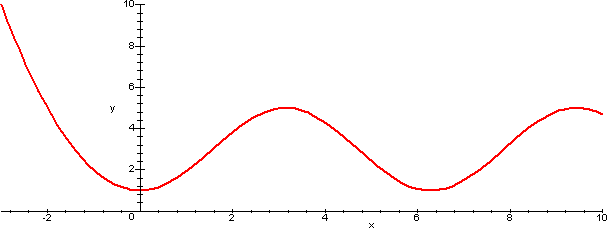
Poiché i parametri sono 4 e abbiamo scritto 4 condizioni, verifichiamone innanzitutto la compatibilità. risolvendo il sistema formato dalle quattro condizioni otteniamo α=0, β=-2, γ=0, δ=3. E' immediato che per questi valori dei parametri la funzione non è ulteriormente derivabile, quindi non potrà essere C4(R) per nessuna scelta dei parametri.
Può essere utile visualizzare il grafico della funzione con i valori ottenuti per i parametri.
Esercizio 3 Sia ![]() , dove
P(x) è un polinomio. Si determini
P(x) il modo tale che la funzione sia di
classe C1(R). Si dica se è
possibile trovare P(x) in modo che la funzione
sia di classe C∞(R).
Poiché i limiti destro in 1 e sinistro in -1 della
funzione sono 0, e poiché un qualunque polinomio è
continuo in 1 e -1, deve essere P(1)=P(-1)=0,
ovvero 1 e -1 devono essere radici del polinomio. Il più
semplice è
P(x)=α(x-1)(x+1). La
derivata destra in 1 e sinistra in -1 valgono 1 e -1. Il
polinomio scelto ha queste derivate se α=1/2. La funzione
così trovata non è di classe
C∞(R), né può
esserlo con qualunque altro polinomio. Infatti, se
P(x) ha grado n, la sua derivata di
ordine n+1 è identicamente nulla, mentre la
derivata di f non è zero né in 1
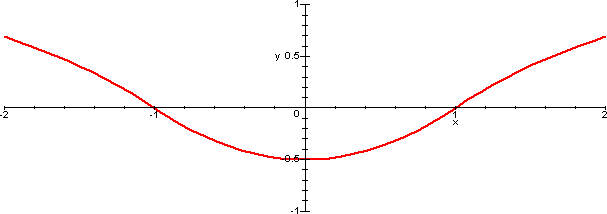
né in -1. Si veda qui sotto il grafico della funzione
corrispondente al polinomio trovato.
, dove
P(x) è un polinomio. Si determini
P(x) il modo tale che la funzione sia di
classe C1(R). Si dica se è
possibile trovare P(x) in modo che la funzione
sia di classe C∞(R).
Poiché i limiti destro in 1 e sinistro in -1 della
funzione sono 0, e poiché un qualunque polinomio è
continuo in 1 e -1, deve essere P(1)=P(-1)=0,
ovvero 1 e -1 devono essere radici del polinomio. Il più
semplice è
P(x)=α(x-1)(x+1). La
derivata destra in 1 e sinistra in -1 valgono 1 e -1. Il
polinomio scelto ha queste derivate se α=1/2. La funzione
così trovata non è di classe
C∞(R), né può
esserlo con qualunque altro polinomio. Infatti, se
P(x) ha grado n, la sua derivata di
ordine n+1 è identicamente nulla, mentre la
derivata di f non è zero né in 1
né in -1. Si veda qui sotto il grafico della funzione
corrispondente al polinomio trovato.
Esercizio 4 Sia 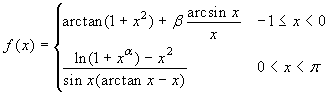 . Dire
per quali valori di α>0 e β si può
prolungare per continuità in 0. Il limite sinistro in 0
è π/4 + β. Calcoliamo il limite destro.
Poiché
. Dire
per quali valori di α>0 e β si può
prolungare per continuità in 0. Il limite sinistro in 0
è π/4 + β. Calcoliamo il limite destro.
Poiché ![]() , si ha:
, si ha: 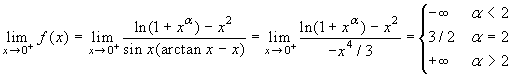 .
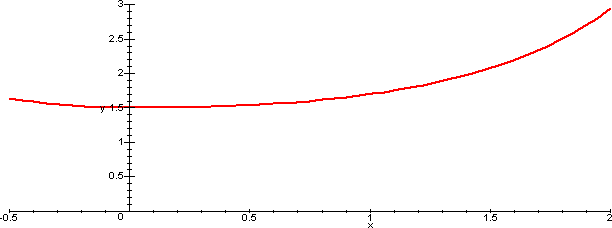
La funzione si può dunque prolungare se α=2 e
β=2-π/4. Si veda qui sotto il grafico della funzione con
i valori trovati dei parametri.
.
La funzione si può dunque prolungare se α=2 e
β=2-π/4. Si veda qui sotto il grafico della funzione con
i valori trovati dei parametri.
Esercizio 5 Dati α, β,
γ, δ, si consideri la funzione ![]() . Per
ogni k≥0 si dica per quali valori di α,
β, γ, δ la funzione è di classe
Ck(R). Si può
ragionare come nell'esercizio 2 qui sopra, ottenendo
α=2, β=-1, γ=1, δ=0. La funzione
così ottenuta non è di classe
C4(R). Si veda qui sotto il grafico
della funzione con i valori trovati dei parametri.
. Per
ogni k≥0 si dica per quali valori di α,
β, γ, δ la funzione è di classe
Ck(R). Si può
ragionare come nell'esercizio 2 qui sopra, ottenendo
α=2, β=-1, γ=1, δ=0. La funzione
così ottenuta non è di classe
C4(R). Si veda qui sotto il grafico
della funzione con i valori trovati dei parametri.