I teoremi di Darboux e sul limite della derivata
Teorema di Darboux
La funzione derivata di una data funzione può essere una funzione molto irregolare, ma ha una importante proprietà in comune con le funzioni continue, come afferma il seguente
Teorema di Darboux. Se
f
è derivabile in [a,b] e se l è un reale compreso tra f'(a) e
f'(b), allora esiste c in ]a,b[ tale che f'(c) = l. In altri termini
la funzione derivata di una funzione assume tutti i valori intermedi compresi tra due suoi
valori.
Questo fatto ha come conseguenza che la funzione derivata di una funzione derivabile in un intervallo non può avere discontinuità a salto: per esempio non esiste alcuna funzione che abbia come derivata la funzione signum. Questa osservazione è della massima importanza quando si affronta il problema della ricerca delle primitive di una funzione (il problema inverso della derivazione).
Teorema sul limite della derivata
Un' altra importante proprietà della funzione derivata di una funzione, molto utile nelle applicazioni, è espressa dal seguente
Teorema. Sia f una funzione
definita e derivabile in un intorno di un punto c escluso il punto c, ma continua
anche in c. Se la funzione f' ha limite finito, per x tendente a
c,
essa è derivabile anche in c e si ha:
.
Questo teorema, in aggiunta al precedente, è di grande utilità, per esempio, per controllare la derivabilità di una funzione che è stata prolungata per continuità in un punto o per controllare la derivabilità di funzioni elementari a tratti.
Esempi
Esempio 1. Dati due reali a e b, si consideri la funzione,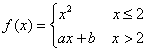 
. Si chiede di determinare, se
possibile, a e b, in modo che la funzione sia ovunque continua e derivabile. I
problemi si possono presentare solo nel punto 2: in un intorno di ogni altro punto la funzione
coincide con una funzione elementare sicuramente continua e derivabile. Avendosi 
, dovrà intanto essere
4=2a+b. Si ha poi, per x≠2, 
. Essendo inoltre 
, se ne deduce che, se a≠4, il limite della
derivata non esiste e la funzione derivata ha una discontinuità di prima specie, per cui non
può essere derivabile in tutto R. Se invece a=4, il limite della derivata
esiste e vale 4: per il teorema sul limite della derivata la funzione è derivabile anche in
2. Poiché 4=2a+b, si conclude che la funzione è continua e derivabile
se a=4 
b=-4.
Osservazione. Nell'esempio precedente si poteva anche calcolare direttamente il
limite del rapporto incrementale per controllare la derivabilità della funzione nel punto 2,
e a volte è indispensabile seguire questa strada come vedremo con l'esempio 2, ma spesso
il calcolo del limite della derivata è molto più agevole che non quello del limite
del rapporto incrementale. In questo caso le difficoltà tecniche erano più o meno le
stesse. Tenendo conto che b=-2a+4 si sarebbe trovato: 
, mentre 
, traendo le stesse conclusioni.
Esempio 2. Si dica se per la funzione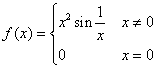 
è applicabile il teorema sul limite della
derivata. Si verifica facilmente che la funzione è derivabile e che: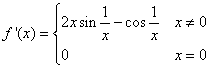 
(per la derivata in 0 si
calcoli il limite del rapporto incrementale). É altrettanto immediato che 
. Questo implica che il teorema
sul limite della derivata non è applicabile. Si noti che questa funzione ha una derivata non
continua, ma che la discontinuità non è a salto, in accordo con il teorema di
Darboux.
Regola pratica
Gli esempi precedenti ci inducono a dedurre la seguente regola pratica: data una funzione continua in un intervallo, se sussistono problemi relativi alla derivabilità in un solo punto x0, si calcolano le derivate per x > x0 e per x < x0; si calcolano poi i limiti di queste derivate (rispettivamente destro e sinistro). Se i limiti esistono finiti ed uguali la funzione é derivabile, se essi sono finiti e diversi la funzione non é derivabile ed ha un punto angoloso; altrimenti occorre procedere al calcolo del limite del rapporto incrementale per verificare la derivabilità o meno. In ogni caso il calcolo del limite del rapporto incrementale é sempre la strada più sicura per controllare la derivabilità, solo che spesso é molto più semplice e veloce procedere come sopra indicato.