Media armonica
Definizione
Dati due numeri a e b, la loro media armonica m
è definita in modo che la sua inversa (1/m) sia
la media aritmetica degli inversi di a e b; si
pone cioè: 
o, il che è lo
stesso, 
. É immediato che la media
armonica può essere calcolata anche con la formula: 
.
Velocità media
Un esempio interessante di applicazione della media armonica è quello della velocità media. Se un corpo si muove da A a B, che distano 80 km, alla velocità di 80 km/h e successivamente da B ad A alla velocità di 20 km/h, quale sarà la velocità media sull'intero tragitto andata-ritorno? Se si facesse la media delle due velocità si otterrebbe 50 km/h. Bisogna però notare che l'intero tragitto è di 160 km, e che viene percorso in 5 ore (1 all'andata e 4 al ritorno): la velocità media corretta è dunque 160/5, cioè 32 km/h, ben diversa dai 50 calcolati con la media aritmetica delle velocità.
In realtà la distanza di 80 km non conta nulla, come mostra il seguente ragionamento. Se si indicano con d la distanza AB, con t1 e t2 i tempi di andata e ritorno, con v1 e v2 le velocità all'andata e al ritorno, allora la media, v, cercata è:
,
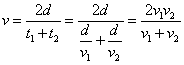che è, come si vede subito, proprio la media armonica
delle due velocità. Questa conclusione è legata al
fatto che il reciproco della velocità rappresenta il
tempo necessario a percorrere l'unità di spazio (una
velocità di 80 km/h significa che mi serve 1/80 di ora
per fare un km!). Se si tiene conto che la velocità media
richiesta si può anche scrivere come 
, il
problema potrebbe essere formulato nel seguente modo: a
quale velocità costante deve muoversi il corpo se si
vuole che il tempo di andata e ritorno sia uguale ed uguale alla
media degli effettivi tempi t1 e t2?
Prezzo medio
Un secondo esempio è legato al concetto di potere di acquisto della moneta. Se un certo oggetto costa oggi 20€ e in un tempo successivo 80€, a quale prezzo dovrebbe essere venduto se si vuole che il potere di acquisto della moneta sia uguale ed uguale alla media dei due poteri di acquisto?.
Per rispondere alla domanda ricordiamo che il potere di acquisto della moneta può essere definito come il reciproco del prezzo: 1/20 (cioè 0.05) rappresenta quanta parte dell'oggetto posso oggi comprare con 1€, 1/80 (cioè 0.0125) rappresenta la frazione di oggetto che posso comprare nel momento successivo sempre con 1€. Per avere il prezzo medio devo dunque calcolare intanto la media dei poteri di acquisto: (0.05+0.0125)/2=0.03125 e poi farne il reciproco, ottenendo 32, risultato che coincide esattamente con la media armonica dei prezzi.
Confronti con le altre medie
Dati due numeri a e b,
si definisce media aritmetica la
loro semisomma, cioè quel numero che, in una
rappresentazione su un asse di ascisse, sta nel mezzo del
segmento individuato dai due numeri: 
.
Questa definizione si può anche riscrivere nel seguente
modo: a-m=m-b o, ancora (a-m):(m-b)=a:a.
Dati due numeri a e b, si definisce media geometrica la radice quadrata del
loro prodotto: 
. Questa definizione
comporta che m è il medio proporzionale tra
a e b: a:m=m:b o, ancora, che
(a-m):(m-b)=a:m.
Anche la media armonica può essere scritta in una forma simile a quella delle medie aritmetica e geometrica. Infatti dalla definizione segue ma+mb=2ab, che si può riscrivere come ma-ab=ab-mb o, ancora, come a(m-b)=b(a-m) ed infine come (a-m):(m-b)=a:b.
Possiamo allora concludere con il seguente schema: dati tre numeri a, m, b, m si dice
- media aritmetica tra a e b se (a-m):(m-b)=a:a.
- media geometrica tra e a e b se (a-m):(m-b)=a:m.
- media armonica tra a e b se (a-m):(m-b)=a:b.
Il numero m è sempre intermedio tra a e b e, se lo indichiamo con ma, mg, mh, a seconda che si tratti della media aritmetica, geometrica od armonica, si ha: ma≥mg≥mh, cioè la media aritmetica è la più grande, quella armonica la più piccola. Le tre proporzioni qui scritte si chiamano anche proporzione aritmetica, geometrica e armonica. La proporzione armonica interviene anche nel problema della divisione armonica di un segmento.
Un po' di storia
Le tre proporzioni furono già considerate dai Pitagorici (circa 500 a.C.). Il nome di armonica fu attribuito, pare, da Archita di Taranto e deriva dal fatto che le corde vibranti che producono l'accordo perfetto do-mi-sol hanno lunghezze che stanno tra di loro in proporzione armonica.