Rettificazione della circonferenza
La rettificazione della circonferenza si basa sul seguente teorema: La circonferenza rettificata è l'unico segmento maggiore del perimetro di un qualunque poligono regolare inscritto nella circonferenza e minore del perimetro di un qualunque poligono regolare circoscritto.
In sostanza la lunghezza della circonferenza è l'estremo superiore dell'insieme dei perimetri dei poligoni regolari inscritti e l'estremo inferiore dell'insieme dei perimetri dei poligoni regolari circoscritti e il teorema precedente si può sintetizzare nell'affermazione che questi due estremi coincidono.
Successivamente si dimostra che il rapporto tra una circonferenza e il suo diametro è una costante, detta π, per cui la determinazione della lunghezza della circonferenza, a partire dal diametro, diventa banale se si riesce a trovare il valore di π.
Purtroppo dopo molti secoli di tentativi si è dimostrato che π è un numero irrazionale (ad opera del matematico svizzero Johan Heinrich Lambert in una memoria presentata all'Accademia di Berlino nel 1761) e addirittura trascendente (ad opera di C.L.F. Lindemann in un articolo pubblicato sui Matematische Annalen del 1882). Queste dimostrazioni portano alla conclusione che non è possibile costruire con riga e compasso un segmento avente la stessa lunghezza di una circonferenza (e ovviamente nemmeno un quadrato avente la stessa area del cerchio).
La prima valutazione, largamente approssimata, del valore di
π, si deve ai Babilonesi che utilizzavano
l'approssimazione π=3. Una valutazione molto più
accurata, e addirittura straordinariamente buona, si deve agli
Egiziani che utilizzavano un quadrato di lato ![]() del diametro per quadrare il cerchio: ciò
significa approssimare π con 3,16, un errore di appena 2
centesimi!
del diametro per quadrare il cerchio: ciò
significa approssimare π con 3,16, un errore di appena 2
centesimi!
Un risultato ancora più accurato venne trovato da Archimede che, operando con poligoni regolari di 6, 12, 24, 48, 96 lati, giunse a stabilire che
![]()
un errore di appena 2 millesimi!.
È utile rendersi conto a livello intuitivo del perché la circonferenza è l'estremo superiore dei perimetri dei poligoni regolari inscritti. Per questo si considerino le figure seguenti:
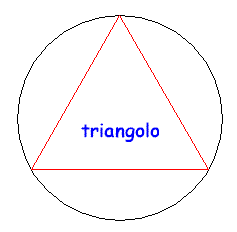
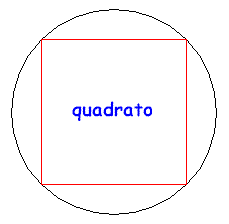
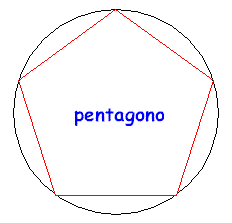
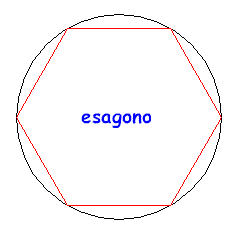
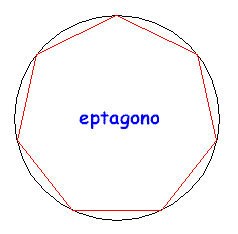
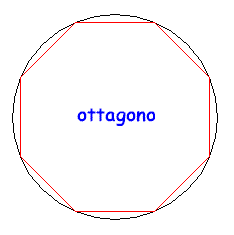
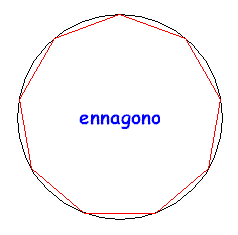
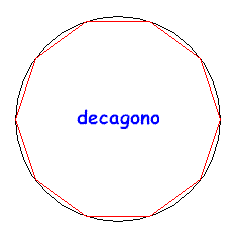
Come si può facilmente capire, all'aumentare del numero dei lati il perimetro del poligono regolare inscritto cresce e si "avvicina" sempre più alla lunghezza della circonferenza, pur rimanendone inferiore. Prendendo un elevato numero di lati si potrà avere una buona approssimazione, per difetto, della lunghezza della circonferenza. Se si fossero considerati i poligoni circoscritti, il perimetro sarebbe diminuito con l'aumentare dei lati e sarebbe sempre rimasto superiore alla lunghezza della circonferenza. Il metodo usato da Archimede si basa proprio sulla determinazione dei perimetri di poligoni inscritti o circoscritti, a partire dall'esagono inscritto che ha, banalmente, perimetro 6r, e per successivi raddoppi del numero dei lati. I calcoli sono comunque estremamente complessi, e l'essere riuscito a portarli a termine è grande merito di Archimede che, probabilmente, aveva anche intuito che, in realtà, si sarebbe potuto trovare il valore di π solo per approssimazioni successive. ( È da ricordare comunque che il simbolo π non venne mai utilizzato dai matematici greci).