Funzione suriettiva
Una funzione si dice suriettiva quando ogni y del codominio è immagine di almeno un punto del dominio. In sostanza ciò significa che tutti i punti del codominio (bersagli) sono colpiti da almeno una delle frecce lanciate dagli arcieri che costituiscono i punti del dominio.
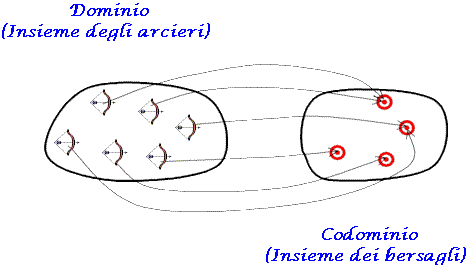
Si
deve esplicitamente osservare che non è affatto escluso
che più frecce colpiscano lo stesso bersaglio, interessa
solo che nessun bersaglio rimanga intatto.
Per le funzioni reali di variabile reale si ha una semplice interpretazione grafica del concetto di funzione suriettiva: una funzione è suriettiva se e solo se il suo grafico gode della proprietà che una retta orizzontale condotta da un qualunque punto del codominio (attenzione: del codominio, non dell'immagine!) interseca il grafico della funzione in almeno un punto.
Nella figura qui sotto è rappresentato il grafico di una funzione suriettiva, con dominio e codominio coincidenti con l'insieme dei numeri reali.
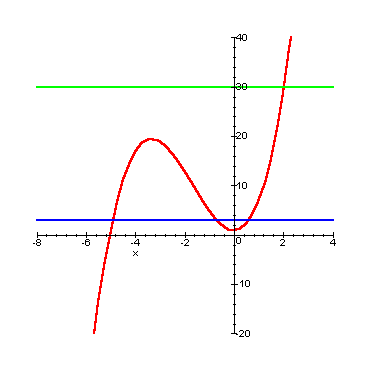
Si noti come la linea orizzontale blu interseca la curva in un tre punti (ciò significa che la funzione non è iniettiva), mentre quella verde la interseca in un solo punto.