Quanto fa (1,001001001...)2?
L'idea di questa pagina nasce dal tentativo di risolvere un "enigma" proposto nel sito dell'Institut de Recherche sur l'Enseignement des Mathématiques, dell'Université Louis Pasteur di Strasbourg.
Ci è parso un esercizio molto interessante sui numeri decimali e sulle difficoltà di calcolo connesse. Come è naturale questi problemi non possono essere sempre risolti dalle calcolatrici o dai calcolatori che possono utilizzare solo un sottoinsieme finito dell'insieme dei reali e che quindi non conoscono i numeri periodici. Si può vedere un interessante esempio elementare delle difficoltà connesse con l'uso di numeri approssimati nei calcolatori.
L'enigma proposto nel sito citato, il mese di aprile 2001, è questo:
Qual è il periodo del numero
decimale ![]() .
.
Se si prova ad impostare il calcolo su una normale calcolatrice tascabile con display a dieci cifre si ottiene 1.002003004 e si capisce subito l'interesse dell'enigma: forse il periodo è proprio 002003004005006...? Ma fino a dove? E manca solo la terna 001?.
Quella che segue è la cronistoria dei tentativi successivi di risolvere l'enigma. Non sapendo da dove partire usiamo un programma per il calcolo simbolico (nel nostro caso Derive perché è in uso nella nostra scuola). Introdotta la frazione 1000000/998001, chiediamo un'approssimazione con 100 cifre e ci accorgiamo che la situazione già presente nella calcolatrice si ripete: le cifre dopo la virgola possono essere raggruppate a 3 a 3, dal gruppo 002 al gruppo 034. Con 1000 cifre si andava dallo 002 al 334, con 2000 cifre fino al 667 più un ulteriore 6. E' solo con 3000 cifre che c'é la prima situazione nuova (visibile solo strabuzzando gli occhi!): i gruppi vanno dallo 002 al 997, poi ci sono i gruppi 999, 000, 001 e un gruppo di due soli zeri alla fine. Provando con 4000 cifre si comincia a ripetere la situazione precedente: tutto concorre a farci credere che il periodo é costituito dalle 2997 cifre ottenute dall'allineamento dei gruppi di 3 cifre inizianti con 002, fino al 997, più i gruppi 999, 000, 001. Manca, per chiudere il cerchio, solo il gruppo 998. Provando con uno sviluppo di 10000 cifre si può, seppure con un po' di pazienza, trovare una conferma a questa congettura. Il predetto "probabile periodo" si ripete per tre volte e mezza.
Ovviamente questa non può essere una prova: sulla base delle note proprietà degli sviluppi decimali dei numeri razionali, il numero in questione può anche avere un periodo costituito da 998000 cifre!!. Anche se Derive ci fa la grazia di rispondere, con qualche minuto di attesa, alla richiesta di un'approssimazione con 1000000 (un milione!) di cifre, ci risulta quasi impossibile effettuare un controllo, anche perché più volte l'applicazione va in blocco quando si fa lo scroll della pagina.
A questo punto decidiamo di adattare a questo caso un vecchio programma Turbo Pascal per il calcolo dei decimali con periodo massimale e, con poco più di un minuto di attesa, il programma ci risponde che effettivamente la nostra idea era giusta: il numero 1000000/998001 è un decimale periodico semplice, con un periodo composto da 2997 cifre, ovviamente coincidenti con quelle offerteci da Derive. Ora però siamo sicuri (?!) della bontà del calcolo perché la risposta del computer é basata sul fatto che il codice, eseguendo la divisione con il metodo a danda, ha trovato un resto che si ripete dopo appunto 2997 passi. La versione Javascript di questo codice si può eseguire on line.
La soluzione presentata, il mese successivo, sul sito dell'Università Louis Pasteur è molto più interessante, in quanto si basa su un calcolo diretto, cioè sulla moltiplicazione, eseguita con la consueta regola, tra i due numeri 1.001001001...! Vogliamo qui trattarla in dettaglio, con lo scopo di mostrare come gli algoritmi tradizionali possano essere vantaggiosamente applicati anche in un'epoca, come la nostra, di dominio quasi assoluto delle macchine automatiche di calcolo.
Il numero che cerchiamo è sicuramente periodico e di poco superiore ad 1, sarà dunque della forma 1,......... possiamo allora evitare problemi con la ricerca della virgola, e semplificare il calcolo scrivendo il numero da quadrare come 001001001.... Cominciamo con un'approssimazione, per esempio con 9 cifre:
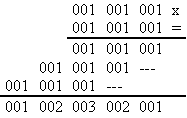 .
.
Nella nostra notazione semplificata questo equivale a scrivere, come risultato: 1.002003002001. Questo primo calcolo ci suggerisce di raggruppare le colonne dei fattori e dei calcoli intermedi della moltiplicazione a 3 a 3: sono tutte colonne con addendi sempre uguale a 001.
Nel caso concreto che vogliamo trattare la moltiplicazione non può essere iniziata, perché si dovrebbe cominciare dall'ultima cifra a destra e, in questo caso, non esiste l'ultima cifra a destra. La moltiplicazione può, però, essere terminata, ottenendo il seguente schema, dove abbiamo anche numerato le righe, a partire dal basso!.
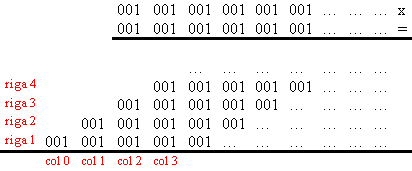
Dobbiamo ora procedere a sommare le colonne, partendo dall'estrema destra. Per fare questo osserviamo che la riga numero 1 (ultima in basso) ci fornirà, come più sopra osservato, la parte che precede la virgola, cioè 1, e non ci potranno essere riporti dalle altre colonne, perché il numero che cerchiamo è proprio della forma 1,...
Consideriamo allora, sempre a partire dal basso, le righe a gruppi di 1000. In sostanza usiamo la proprietà associativa: somma=(somma righe 1-1000) + (somma righe 1001-2000) + .... Solo per i più raffinati osserviamo che la cosa è sicuramente lecita perché il numero che stiamo cercando può essere considerato come la somma di una serie assolutamente convergente: 1.001001001...+0.000001001...+0.000000001....
Cominciamo col considerare le prime 1000 righe a partire dal basso: otteniamo il seguente schema:

In sostanza la 1000 colonna è influenzata dai riporti di tutte le colonne alla sua destra e influenza, con i suoi riporti, le due colonne a sinistra. Il gruppo 998 non compare.
Se ora consideriamo il secondo gruppo di 1000 righe, sempre a partire dal basso, possiamo concludere che avrà le prime colonne (di 3 cifre ciascuna!) con spazi vuoti e le successive ripeteranno esattamente lo schema sopra riportato. Potremo scrivere come somma delle righe dal 1001 al 2000:
![]() .
.
I gruppi successivi saranno costruiti sullo stesso principio.
Potremo ora procedere ad un successivo raggruppamento, sempre a 1000 a 1000, di questi gruppi che ora abbiamo sommato. Puoi anche vedere lo schema del raggruppamento dei primi gruppi di 1000 righe, a partire dal basso. Per rendere più leggibile la tabella abbiamo anche raggruppato le colonne a 1000 a 1000.
Come si può vedere il 1000° gruppo di 1000 colonne è influenzato dai riporti delle colonne che lo seguono a destra ed influenza, con i suoi riporti, solo i due gruppi alla sua sinistra e non gli altri. Se procediamo calcolando la somma di 1000 di questi gruppi di righe, lo schema si ripeterà.
Teniamo ora conto dei seguenti fatti:
- Il nostro numero, avendo denominatore 998001, avrà una rappresentazione decimale con non più di 998000 cifre nel periodo.
- Il gruppo 002003...996997999000001 (di 2997 cifre) si ripete in questo risultato per più di 990 volte fornendo almeno 2967030 cifre che non potranno essere influenzate dai riporti delle somme delle colonne e righe che rimangono.
Questo ci permette di concludere, senza l'uso di
calcolatrici o programmi al computer, e senza eseguire
manualmente la divisione, che ![]() . Un bel periodo,
sia come lunghezza che come forma!!
. Un bel periodo,
sia come lunghezza che come forma!!
Una curiosa domanda che può sorgere a questo punto
è: qual è la frazione generatrice del numero
decimale periodico ![]() ?. Questo
numero differisce dal nostro numero solo a partire dalla
2991a cifra dopo la virgola e, quindi, è
pochissimo diverso da esso. Chissà se la sua frazione
generatrice
?. Questo
numero differisce dal nostro numero solo a partire dalla
2991a cifra dopo la virgola e, quindi, è
pochissimo diverso da esso. Chissà se la sua frazione
generatrice
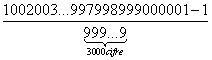
è facile da semplificare!