Sulla definizione di seno e coseno
L'introduzione delle funzioni circolari, a livello elementare, non è agevole e, nella pratica, queste funzioni vengono definite facendo ricorso a concetti facili da intuire, ma non facili da spiegare in maniera rigorosa, tra cui il concetto di senso orario e senso antiorario, che non hanno alcun significato matematico.
Le funzioni circolari sono in realtà strettamente legate alle funzioni esponenziali, ma questo fatto può essere compreso solo lavorando nel campo complesso.
É possibile comunque una introduzione sufficientemente "pulita" anche rimanendo nell'ambito reale se si ammette di poter utilizzare i concetti di archi di cerchio e di lunghezza dei medesimi, nonché il fatto che la lunghezza della circonferenza e l'area del cerchio sono date, rispettivamente, dalle formule 2πr e πr2; l'unico problema è che occorre far ricorso al calcolo differenziale. L'idea qui esposta è presa da Barozzi, E., Gonzalez, E., Calculus, Libreria Progetto, Padova 1989.
Procediamo dunque con queste ipotesi e consideriamo, in un
sistema di coordinate cartesiane ortogonali, la
semicirconferenza di centro l'origine e raggio 1, avente
equazione 
.
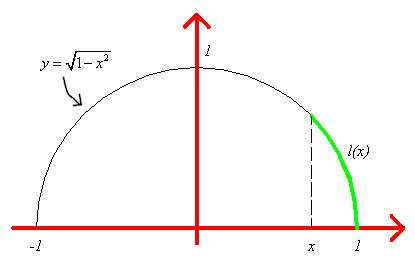
Indichiamo con l(x) la
funzione "lunghezza dell'arco" rappresentato nella
figura qui sotto. La funzione l ha dominio [-1,1] e
gode delle seguenti proprietà: l(1)=0, l(0)=π/2,
l(-1)=π. Non ci interessa tanto trovare
un'espressione per la funzione, quanto calcolare la sua
derivata. Per far questo dobbiamo considerare il rapporto
incrementale 
e poi far tendere h a zero.
La dimostrazione che ci proponiamo di fare è basata sul
teorema dei carabinieri, per cui intendiamo
"incastrare" la quantità di cui vogliamo il
limite tra altre due che abbiano lo stesso limite. Cominciamo a
considerare h<0 e, con riferimento alla figura qui
sotto, indichiamo con A il punto della semicirconferenza di
ascissa x, con B quello di ascissa x+h, con C
il punto, di ascissa x+h, sulla tangente in A alla
semicirconferenza, e osserviamo che si ha: 
.
Indichiamo con γ la lunghezza dell'arco 
. Si ha, come è ben noto,
AB<γ.
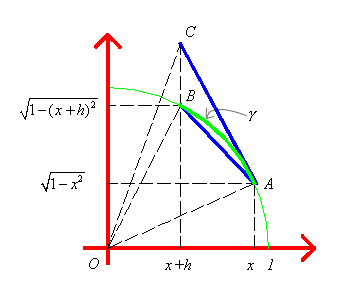
Poiché la circonferenza ha raggio 1, l'area del settore circolare OAB vale γ/2 e tale area risulta minore di quella del triangolo OAC che vale AC/2. Ne segue γ<AC. Dunque AB<l(x+h)-l(x)<AC. Tenendo conto che h<0 possiamo concludere che:
.
Se si calcolano i limiti dei due "carabinieri", 
e 
, si ottiene il valore
comune 
.
Un discorso perfettamente identico si può fare se h>0 (basterà qualche semplice adattamento). Si può quindi concludere che
.
Il calcolo di questa derivata ci consente di affermare che la funzione l è strettamente decrescente (la cosa è, d'altro canto, evidente anche a livello intuitivo) nel suo dominio, per cui risulterà invertibile. Ciò significa che, per ogni s dell'intervallo [0,π] , esiste un unico x dell'intervallo [-1,1], tale che l(x)=s. Chiameremo funzione coseno, che indicheremo semplicemente con cos, l'inversa della funzione l, cioè porremo, per definizione,
.
Definiremo poi la funzione seno, che indicheremo semplicemente con sin, con lo stesso dominio e codominio del coseno, mediante la posizione:
.
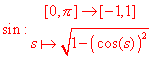La regola di derivazione della funzione inversa ci consente di ricavare facilmente che:
.
Assieme alla formula 
, che si ricava banalmente
dalla definizione, questo è quello che conta sapere sulle
funzioni seno e coseno.
Si possono prolungare le funzioni all'intervallo [-π,0], ponendo cos(-s)=cos(s) e sin(-s)=-sin(s). Per avere funzioni definite su tutto l'insieme dei reali è poi possibile estenderle per periodicità. Per le funzioni così ottenute si usa ancora lo stesso nome di funzione seno e coseno.
Per concludere lo studio delle funzioni seno e coseno occorre
naturalmente ricavare le formule di addizione e sottrazione, in
particolare la formula
cos(x-y)=cos(x)cos(y)+sin(x)sin(y), da cui poi tutte le
altre si possono ricavare. Il problema si può ricondurre
a quello di mostrare che la funzione coseno è l'unica
che soddisfa alle condizioni: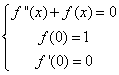 
. Per chi vuole
approfondire l'argomento rimandiamo al citato testo di
Barozzi Gonzalez. Qui ci preme segnalare solo che questo modo di
procedere, seppure un po' pesante dal punto di vista
formale, consente un'introduzione abbastanza pulita delle
funzioni trigonometriche rimanendo nell'ambito reale e,
soprattutto, consente di introdurre queste funzioni senza mai
far ricorso al concetto di angolo: nelle applicazioni il fatto
che la trigonometria possa anche servire a "risolvere"
certi problemi sui triangoli è un fatto, tutto sommato,
piuttosto secondario. Anzi la cosa essenziale è proprio
il fatto che la funzione coseno è l'unica funzione,
con opportune condizioni iniziali, la cui derivata seconda
è opposta alla funzione stessa: si pensi per esempio
all'equazione differenziale dei moti armonici, da cui hanno
origine praticamente tutte le applicazioni delle funzioni
trigonometriche.