La bottiglia di Klein
La bottiglia di Klein è un esempio molto interessante di superficie a una sola faccia che, a differenza del nastro di Möbius, è anche una superficie chiusa, cioè "priva di contorno". Purtroppo questa superficie ha il suo ambiente naturale in uno spazio a quattro dimensioni e quindi non è possibile darne una visualizzazione corretta nel nostro povero spazio geometrico a tre dimensioni. Se però ci accontentiamo di uno "schiacciamento" di questa superficie in modo da poterla incapsulare nello spazio a tre dimensioni, allora ci sono varie rappresentazioni, che in ogni caso rendono evidente la proprietà di questa superficie di avere una sola faccia e di essere chiusa: come già succede se vogliamo schiacciare il nastro di Möbius nello spazio a due dimensioni questo "schiacciamento" produrrà delle "complicazioni", in questo caso una intersezione della superficie con se stessa.
Tra i possibili incapsulamenti tridimensionali della bottiglia di Klein, mostriamo quello proposto dallo stesso Felix Klein (1849-1925). Per costruirlo consideriamo una superficie di forma cilindrica, più stretta da un lato.
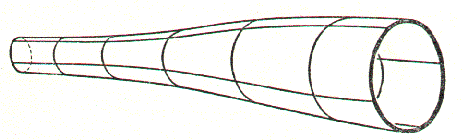
Supponiamo ora di voler fare combaciare le due estremità, ma non in modo da ottenere un toro, bensì praticando un foro nella parete del cilindro e infilandoci l'estremità più sottile, come è indicato nella figura qui sotto.
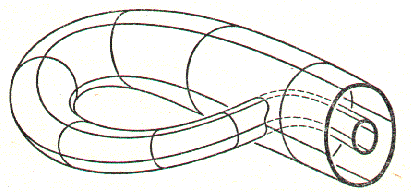
Se completiamo il procedimento otterremo la superficie che stiamo cercando, la "Bottiglia di Klein", o meglio un suo incapsulamento nello spazio tridimensionale.
Si tratta di una superficie ad una sola faccia, cioè con la proprietà che da qualunque punto sulla superficie si può raggiungere qualunque altro punto (esattamente come nel nastro di Möbius), ma con l'ulteriore interessante proprietà di essere una superficie chiusa, cioè priva di bordi. L'immersione della bottiglia nello spazio a tre dimensioni ha introdotto una linea di intersezione tra due parti della superficie.
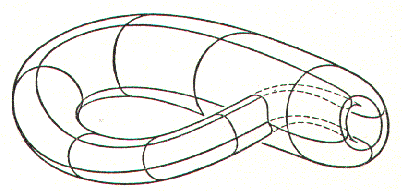
Se tagliamo la bottiglia di Klein lungo una linea mediana otteniamo due nastri di Möbius: un altro modo di costruire la bottiglia è proprio quello di saldare due nastri di Möbius per il loro bordo. Il fatto che la bottiglia di Klein contenga nastri di Möbius è di particolare interesse: il nastro di Möbius può essere considerato come l'unità base delle superfici non orientabili (cioè con una sola faccia), in quanto si può provare che ogni superficie di questo tipo contiene un nastro di Möbius.

Anche se è un po' più difficile da disegnare si può provare che la bottiglia di Klein potrebbe essere trasformata in un unico nastro di Möbius con un taglio lungo una linea chiusa opportuna.