Il nastro di Möbius
Le superfici "ordinarie", cioè quelle che capitano di solito sotto i nostri occhi, hanno due facce, e questo vale sia per le superfici chiuse (cioè prive di contorno), come la sfera, che per quelle aperte (cioè delimitate da curve), come un rettangolo. Questo significa che, per le superfici chiuse, è possibile colorare le due facce con colori diversi senza che ci sia alcun punto di incontro tra i due colori, per le superfici aperte che i due colori possono incontrarsi solo lungo i bordi.
Se per esempio consideriamo un rettangolo e immaginiamo di disporre una formica su una delle due facce e del cibo sull'altra, se provvediamo a spargere dell'insetticida lungo tutto il bordo, la formica non potrà mai raggiungere il cibo (a meno che non faccia un buco nel rettangolo!). Similmente se consideriamo una mosca fuori da una sfera di cristallo e del cibo posto all'interno della sfera stessa, la mosca non riuscirà mai a raggiungere il cibo. Ebbene, esistono anche superfici con una sola faccia (e superfici chiuse che non hanno un "dentro" e un fuori", per esempio la bottiglia di Klein): l'esempio più classico è il nastro di Möbius.
L'idea base della costruzione è molto semplice, come puoi vedere seguendo i passi indicati qui sotto.
|
|
|
|
|
|
| uno | due | tre | quattro | cinque |
Il nastro così ottenuto si chiama di Möbius, in onore di A.F.Möbius (1790-1860) che per primo lo considerò. Questa superficie ha l'interessante proprietà di avere un'unica faccia (e anche un solo bordo): la nostra formica potrebbe raggiungere il cibo senza pericolo in qualunque posto del nastro si trovi. Per dipingere una figura come questa, se non si vogliono contatti tra i colori, bisogna usare un solo colore e allora basta immergere tutto il nastro nel barattolo di vernice, con grande risparmio di tempo. Si noti che, se avessimo congiunto i lati AB e CD, ma senza torsione, facendo coincidere A con D e B con C, si sarebbe ottenuta una superficie cilindrica, ancora con due facce, per cui alla nostra formica non rimaneva altro che bucare il foglio per raggiungere il cibo.
Ci sono altre proprietà interessanti di questa superficie. Segnaliamo questa: se si taglia la superficie lungo la linea mediana, si ottiene un unico pezzo, a differenza di quello che si ottiene se si taglia in due la superficie cilindrica che si ottiene piegando il quadrato nel modo "tradizionale", cioè senza torsione, in modo che A vada a coincidere con D e B con C. Buon divertimento e, a proposito, che cosa succede se al lato CD si fa fare una torsione completa (cioè un giro intero e non mezzo come abbiamo fatto noi), in modo che A vada sempre a coincidere con D e B con C?.
É molto importante l'osservazione che il nastro di Möbius non si può incapsulare nel piano evitando intersezioni delle sue parti: basta provare a costruire un modello di carta per poi schiacciarlo fino a farlo diventare piatto, si otterrà una figura del tipo rappresentato qui sotto.
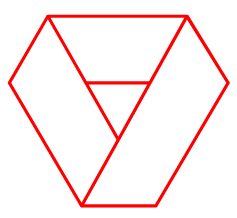
In ogni caso, anche se lo schiacciamento in due dimensioni del nastro produce una figura con parti che si sovrappongono, è comunque possibile, da questa rappresentazione bidimensionale, ricavare la proprietà essenziale della figura di essere ad una faccia: basterà immaginare che anche la nostra formica che insegue il cibo sul nastro sia stata schiacciata (senza farle del male naturalmente!) fino a farla diventare un essere piatto come gli abitanti di Flatland.
Si noti che per il cilindro la situazione è diversa: mentre è ovvio che schiacciandolo si ottiene anche qui una figura con parti che si intersecano, nel cilindro non si modifica sostanzialmente nulla se lo si taglia lungo una generatrice e poi lo si stende sul piano (la geometria del cilindro è sostanzialmente la stessa di quella del piano).
La considerazione che il nastro di Möbius, se schiacciato nel piano, ha delle parti che si sovrappongono diventa particolarmente importante nel caso della bottiglia di Klein, per la quale si può produrre solo una immagine del suo incapsulamento nello spazio tridimensionale, dove sono presenti parti che si intersecano: nel suo "spazio naturale", che è a quattro dimensioni, non ci sarebbe alcuna intersezione, esattamente come non c'è alcuna sovrapposizione se mantengo il nastro di Möbius nel suo "spazio naturale", che è quello a tre dimensioni.
Puoi vedere una costruzione animata di questo nastro.