Numeri perfetti e numeri di Mersenne
Sono perfetti i numeri naturali che sono la somma dei loro divisori. Il primo numero perfetto è 6=1+2+3.
Euclide riuscì a dimostrare, nel libro IX dei suoi elementi, Proposizione 36, che:
Se quanti numeri si voglia, a partire dall'unità, sono formati con una successione a doppia proporzione fin quando la somma di tutti è un primo, e se formiamo un numero moltiplicando questa somma per l'ultimo dei numeri, allora questo prodotto è perfetto.
In termini di notazioni moderne si può scrivere: un
numero della forma 
è perfetto se 
è primo. Infatti, usando la formula per la somma
di una progressione
geometrica di ragione 2, si ottiene facilmente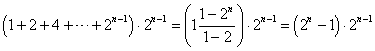 
.
La dimostrazione di questo fatto è abbastanza semplice.
Se è primo gli unici divisori di p
diversi da p, sono i seguenti: 
e
. Non è difficile calcolarne la somma, con
la regola relativa alle progressioni geometriche, e verificare
che tale somma è p.
É un grosso merito di Euclide l'essere riuscito a completare la stessa dimostrazione solo con metodi geometrici.
Eulero, 2000 anni dopo Euclide, riuscì a dimostrare che la condizione è anche necessaria se ci limitiamo ai perfetti pari. Per i dispari non si sa ancora nulla, ma tutti i prefetti finora trovati sono pari, e si sa che se un perfetto dispari esiste deve essere più grande di 10300.
I numeri della forma sono detti numeri di Mersenne ed indicati con
Mn. In generale questi numeri non sono
primi, nemmeno se n è primo ( per esempio
M11=2047=89·23). Il più grande numero
di Mersenne primo, fino a qualche anno fa, (1998) era
M3021377. Non si sa nemmeno se di numeri di Mersenne
primi ce ne siano un numero finito o se siano infiniti.
Potete anche visualizzare un programma javascript per generare numeri perfetti, con qualche ulteriore informazione non contenuta in questa pagina..