Il calcolo del numero di chicchi di grano
Il calcolo del numero di chicchi di grano non è difficile
se si conoscono le progressioni
geometriche. I chicchi, sulle caselle numerate da 0 a
63, sono 20, 21, 22, ...,
263. Applicando la formula per la somma dei termini
di una progressione geometrica di ragione 2 si ottiene: 
, cioè all'incirca 18 trilioni e mezzo
(18 e mezzo miliardi di miliardi!).
C'è però un modo assai più semplice per arrivare al risultato. Cominciamo con il richiamare due importanti formule per la scomposizione in fattori di una somma o una differenza di potenze di ugual esponente.
-
.
-
.
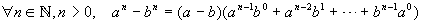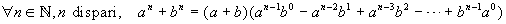Se applichiamo ora la prima di queste formule al caso
a=2, b=1, n=64 otteniamo: 
. Da qui si ricava immediatamente lo stesso
risultato di sopra.
Queste due formule di scomposizione rivestono grande importanza in numerose situazioni e vale la pena di avere approfittato di Dante per rivederle!
Vale la pena di ricordare che le due formule sopra riportate non escludono altre formule o tecniche per scomporre somme e differenze di potenze con ugual esponente, come si può vedere con alcuni esempi.
-
.
-
.
-
.
-
.
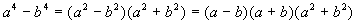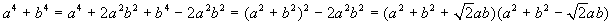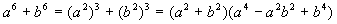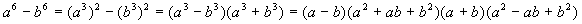E' difficile immaginare quanto sia grande il numero di chicchi di grano ottenuto dai calcoli precedenti. Per questo proponiamo di distribuire i chicchi idealmente sulla superficie terrestre per calcolarne la densità.
Se volete rendervi conto in un altro modo della enormità dei numeri coinvolti nel calcolo dei chicchi di grano, provate ad immaginare di mettere sulla prima casella della tastiera una moneta da 1 euro, sulla seconda 2 monete, sulla terza 4, e così via e chiedetevi quanto sarà alta la pila di monete sulla sessantaquattresima casella (1 moneta da 1 euro ha uno spessore di circa 2 mm.). Il conto è presto fatto: nella sessantaquattresima casella ci sono 263 monete che, moltiplicando per 2 mm., danno una colonna alta 18 446 744 073 709 551 616 mm., ovvero circa 18500 miliardi di chilometri, una distanza pari a circa 2 anni luce, la metà della distanza tra la terra e Proxima Centauri, la stella più vicina a noi, dopo il sole!