Il caso di un punto e una circonferenza
Il luogo dei punti equidistanti da un punto ed una circonferenza.
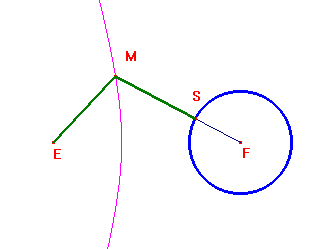
Sono dati un punto E ed una circonferenza di centro F e raggio r, e supponiamo che E sia esterno alla circonferenza. Si tratta di trovare il luogo dei punti M tali che ME=MS. Essendo MS=MF-r. Se ne deduce che deve essere MF-ME=r, cioè che il luogo richiesto è un ramo di iperbole avente fuochi nei punti E ed F dati.
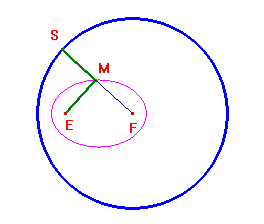
Se invece il punto E è interno alla circonferenza, da ME=MS si ottiene ME=r-MF, e infine ME+MF=r. Si tratta di un'ellisse di fuochi E ed F.
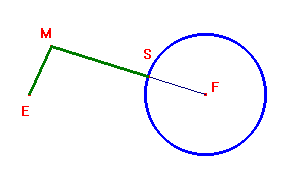
Il luogo dei punti aventi distanze da un punto ed una circonferenza in rapporto dato.
Con riferimento alla figura di seguito siano dati un punto E ed
una circonferenza di centro F e raggio r. Si tratta di
trovare il luogo dei punti M tali che 
ovvero 
. Si deduce subito che
MF-kME=r. Il luogo è dunque un'ovale di
Cartesio.
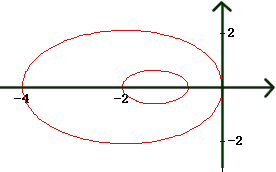
Non ci sono sostanziali variazioni se il punto è interno alla circonferenza. A titolo d'esempio riportiamo qui sotto il grafico, ottenuto con Derive, del luogo, nel caso la circonferenza abbia raggio 1 e la distanza MS sia doppia di ME: MF-2ME=1.
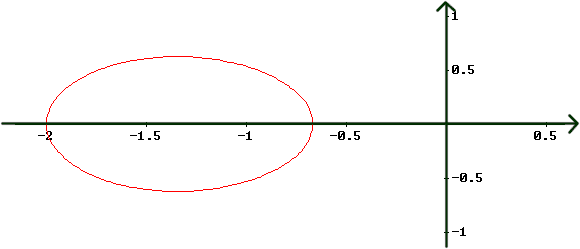
Il grafico è stato tracciato determinando l'equazione
cartesiana del luogo, dopo aver posto i fuochi nei punti (-1,0)
e (1,0). Con due elevazioni al quadrato si ottiene
un'equazione in due incognite di quarto grado, 
, comprensiva del luogo richiesto e di
un'altra ovale, corrispondente al caso MF-2ME=-1.
Il grafico di questa equazione è rappresentato nella
figura qui di seguito.
