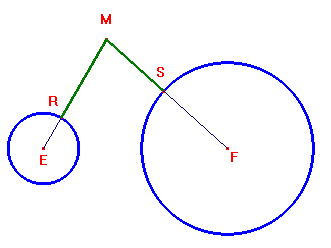
Il caso di due circonferenze
Il luogo dei punti equidistanti da due circonferenze
Non ci sono sostanziali differenze rispetto al caso di un punto e una circonferenza. Con riferimento alla figura di seguito, riferita al caso di circonferenze non interne una rispetto all'altra, indichiamo con r1 ed r2 i raggi delle due circonferenze (di centri E ed F rispettivamente). Il luogo cercato è tale che MR=MS, ovvero ME-MF=r1-r2. Si tratta di un ramo d'iperbole (eventualmente una retta se le due circonferenze hanno lo stesso raggio).
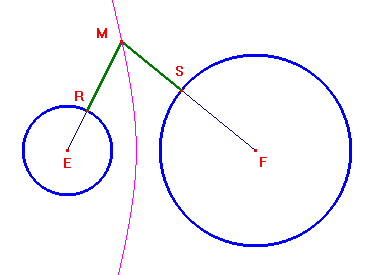
Se invece le due circonferenze sono una interna all'altra, da MR=MS si ottiene ME-r1=r2-MF ed infine ME+MF=r1+r2, ovvero un'ellisse di fuochi E ed F.
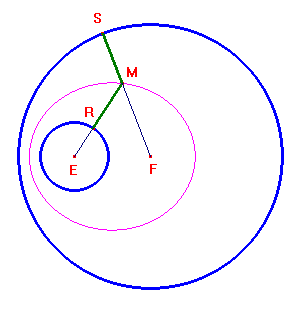
Il luogo dei punti con distanze in rapporto dato da due circonferenze.
Anche ora non ci sono sostanziali differenze rispetto al caso di
un punto ed una circonferenza: se il punto M è esterno
alle due circonferenze, da 
si ottiene 
, ovvero
ME-kMF=r1-kr2. Solo un piccolo
adattamento è necessario se si cercano anche punti M
interni ad una delle due circonferenze, o se le due
circonferenze sono una interna all'altra. Si tratta sempre
di un'ovale di Cartesio.
