Compassi e dimensione
Un sistema sostanzialmente identico al metodo del box counting, ma molto più utile soprattutto nel caso delle linee, è quello che porta al cosiddetto concetto di compass dimension.
L'idea è la seguente. Supponiamo di avere una linea e un regolo rigido di determinata lunghezza, s. A partire dal primo punto della linea riportiamo il regolo (con un compasso) e consideriamo la sua intersezione (unica in questa fase preliminare di approccio al problema) con la linea stessa. Ripetiamo l'operazione a partire da questa intersezione fin quando "ricopriamo" tutta la linea. L'ultimo passaggio potrebbe anche richiede una parte non intera del regolo. Indichiamo con N(s) il numero di regoli che ci sono serviti. Ripetiamo l'intero processo con regoli via via più piccoli. Se si esamina la figura qui sotto si può notare che, per la misura della curva proposta, con il regolo più lungo servono un po' più di due regoli e mezzo, con quello più corto 7 regoli.
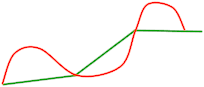

E' chiaro che quanto più il regolo è corto, tanto più la misura sarà precisa.
Applichiamo ora questo procedimento ad un segmento lungo 2, a una semicirconferenza di diametro 1, all'insieme di Cantor, e al merletto di Koch. Per semplicità di calcolo sceglieremo di ridurre le dimensioni del regolo iniziale, che prendiamo uguale ad uno, di fattori diversi a seconda dei casi. Riportiamo i risultati in una tabella. Tranne che per la semicirconferenza la costruzione della tabella è banale e non richiede commenti. Puoi vedere i semplici dettagli sulla costruzione relativa alla semicirconferenza. Nella tabella abbiamo riportato anche la lunghezza che si ottiene, al variare di s.
| Livello | Segmento | Semicirconferenza | Insieme di Cantor | Merletto di Koch | ||||||||
| s | N(s) | L(s) | s | N(s) | L(s) | s | N(s) | L(s) | s | N(s) | L(s) | |
| 0 | 1 | 2 | 2 |
1= |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 |
|
4 | 2 |
|
2 | ≈1.4142 |
|
2 | ≈0.6666 |
|
4 | ≈1.3333 |
| 2 |
|
8 | 2 |
|
3 | 1.5 |
|
4 | ≈0.4444 |
|
16 | ≈1.7778 |
| 3 |
|
16 | 2 |
|
4 | ≈1.5307 |
|
8 | ≈0.2962 |
|
64 | ≈2.3704 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 100 | ≈0 | ≈1030 | 2 | ≈0.0157 | 101 | ≈1.5707 | ≈0 | ≈1030 | ≈0 | ≈0 | ≈1060 | ≈1012 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| n |
|
2n+1 | 2 |
|
n |
n × |
|
2n |
2n × |
|
4n |
4n × |
E' chiaro che, in tutti i casi, la lunghezza è stata ottenuta moltiplicando il numero di regoli per la lunghezza del regolo: L(s)=N(s)×s. Esaminando la tabella si può osservare come L, nel caso del segmento, sia costante mentre nel caso della semicirconferenza subisce all'inizio variazioni sensibili per poi stabilizzarsi intorno a valori prossimi a 1.57 (naturalmente coincidente con il valore previsto di π/2). Nel caso dell'insieme di Cantor o del merletto di Koch la lunghezza tende invece, rispettivamente, ad annullarsi o a divergere senza limiti. Ma questi fatti ci erano già noti. Ora vogliamo ricavare dalla tabella qualche altra informazione.
La formula L=Ns, stabilisce un ovvio legame tra il numero di regoli utilizzati e la lunghezza dei regoli stessi. Questo legame è di proporzionalità inversa per il segmento, in quanto Ns è costantemente uguale alla lunghezza del segmento: possiamo scrivere Ns=k o, meglio N=ks-1 (k è la lunghezza del segmento, ma questo è, per quanto vogliamo dire, poco importante). Nel caso della semicirconferenza il legame non è esattamente di proporzionalità inversa, perché L aumenta al diminuire di s: poiché però tali aumenti sono sempre più piccoli all'aumentare del livello, possiamo affermare che il legame è tendenzialmente di proporzionalità inversa. In altre parole, pur di prendere s abbastanza piccolo, potremo concludere che Ns è approssimativamente costante e uguale a circa 1.57, o anche che N≈ks-1, esattamente come nel caso del segmento. Si tratta di un risultato abbastanza evidente e prevedibile: se diminuiamo la lunghezza del regolo, dovremo aumentare circa proporzionalmente il numeri di regoli utilizzati per coprire tutta la linea.
Se invece di una linea avessimo considerato una superficie, come un quadrato o un cerchio, avremmo dovuto utilizzare quadrati di lato uguale alla misura del regolo per calcolare la superficie. Indicando con N il numero di quadrati utilizzati, si sarebbe trovato il seguente legame tra N ed s (lunghezza del regolo): N=ks-2, con k esattamente uguale all'area se applichiamo il procedimento ad un quadrato, variabile, ma tendente rapidamente al valore dell'area, se applichiamo il procedimento ad un cerchio.
La cosa che ci interessa in questa formula è l'esponente di s: -1 per il segmento o la semicirconferenza (in generale per una linea nel senso comune del termine), -2 per una superficie ordinaria. Poiché questi numeri sono esattamente la dimensione topologica di una linea e di una superficie, potremo concludere che, nel caso di figure "normali" vale il seguente legame tra il numero N di "unità di misura" e la taglia lineare s dell'unità stessa:
N≈k ×s-D
ove D è la dimensione (1, 2 o 3) della figura.
Se esaminiamo ora il caso dell'insieme di Cantor o del
merletto di Koch, ci accorgiamo subito che non esiste più
alcun legame di proporzionalità inversa tra N ed
s: nel primo caso Ns tende a zero, nel secondo
all'infinito. Possiamo però sempre chiederci se
esiste un qualche altro legame tra N ed s che
possa condurre ad una formula del tipo di quella valida per
le curve normali. La ricerca di questo legame ha esito
positivo e si trova che, per l'insieme di Cantor, si ha
N≈s-0.63, mentre per il
merletto di Koch si ha
N≈s-1.26. Addirittura per
questi due insiemi la formula può essere scritta
esattamente come ![]() e
e ![]() per
Cantor e Koch rispettivamente. La verifica di questo fatto è immediata
per chi conosce i logaritmi.
per
Cantor e Koch rispettivamente. La verifica di questo fatto è immediata
per chi conosce i logaritmi.
Possiamo dunque concludere che, anche nel caso di situazioni "patologiche" come l'insieme di Cantor e il merletto di Koch, esiste una relazione del tipo N≈ks-D, tra il numero di regoli e la misura del regolo. Questo fatto ci porta a interpretare l'esponente, cambiato di segno, di s come una sorta di dimensione. Si può fare la seguente ulteriore osservazione. Poiché Ns rappresenta la lunghezza della curva in questione, variabile al variare di s, possiamo affermare che, perlomeno per una larga classe di curve, incluse alcune situazioni patologiche, esistono due costanti k e D tali che:
L(s)≈k ×s1-D.
Il numero D può coincidere oppure no con la dimensione topologica della curva, e si chiama compass dimension della curva stessa.
La cosa interessante in tutto questo è che estesi e importanti lavori sperimentali di Lewis Fry Richardson, ripresi e discussi da Mandelbrot, provano che una relazione di questo tipo vale sempre per la lunghezza delle coste degli stati. Per esempio nel caso della Gran Bretagna si trova una relazione di quel tipo con D≈1.24, nel caso dell'Islanda con D≈1.27, nel caso del Sud Africa con D≈1.04, nel caso del Portogallo con D≈1.12. Questo numero interpreta dunque molto bene il livello di frastagliatura delle coste.
Puoi vedere indicazioni sulla tecnica utilizzata per il calcolo di D in situazioni reali .
Anche in questo caso si può parlare di dimensione frattale, con le avvertenze già segnalate nel caso della dimensione definita per autosimilarità.
Le considerazioni svolte in questa pagina ci consentono di dare una risposta al famoso quesito di Mandelbrot: "Quant'è lunga la costa della Gran Bretagna?". La risposta che pare più adeguata è: la lunghezza della costa della Gran Bretagna non è fissa, ma dipende dall'uso che voglio farne. Se per esempio volessimo recintare la Gran Bretagna con una rete metallica, piazzando un palo di sostegno ogni 10 metri otterremmo un certo numero (che ci serve per valutare quanti metri di rete e quanti pali dobbiamo comprare); se invece dovessimo costruire una rete di protezione con dei radar piazzati su pali ogni 10 km, otterremmo un numero diverso (che ci serve per sapere quanti radar installare), e non c' proporzionalità tra l'aumento della distanza tra i pali e la diminuzione nel numero dei pali. Se la Gran Bretagna fosse un quadrato di lato 10 km, utilizzerei 4000 paletti nel primo caso e 4 pali per i radar nel secondo (piazzandoli per esempio ai vertici del quadrato), con una rapporto 1000 a 1, esattamente inverso a quello, 1 a 1000, nella misura del regolo.