La scala diabolica
Utilizzando l'insieme di Cantor e la sua rappresentazione in
base 3 è possibile definire una funzione 
, dotata di straordinarie proprietà. Cominceremo a
definirla sull'insieme di Cantor e poi la estenderemo a
tutto [0,1]. Se x è un elemento di C,
sia 0,a1a2a3... la sua
scrittura in base 3, in cui gli ai sono solo
0 oppure 2. Poniamo ora
.
L'immagine di x si ottiene cioè sostituendo
tutti i 2 della scrittura ternaria con degli 1, e interpretando
il numero così ottenuto in base due. La funzione non
è iniettiva, anzi si può provare che sugli estremi
di ciascuno degli intervalli cancellati per ottenere
l'insieme di Cantor essa assume gli stessi valori. Lo
proveremo per esempio sul primo intervallo di estremi 1/3 e 2/3.
Si ha 
, 
. Però è suriettiva. Infatti ogni numero di
[0,1] può essere scritto, in forma binaria, con una
scrittura del tipo 0,b1b2...e tale numero
è di certo l'immagine dell'elemento
dell'insieme di Cantor che si scrive, in forma ternaria,
sostituendo tutti gli 1 con dei 2. Inoltre è una funzione
(debolmente) crescente. Se infatti x< y
sono due punti di C, con rappresentazioni ternarie
0,a1a2a3... e
0,b1b2b3..., sia n il
primo indice delle cifre dopo la virgola per cui i due numeri
differiscono. Deve essere, necessariamente,
an=0 e bn=2. I due
numeri sono allora
0,a1a2...an-10an+1...
e
0,a1a2...an-12bn+1...;
per le immagini si ha:
,
da cui la conclusione. La funzione f si può facilmente estendere a tutto [0,1] ponendola costante ed uguale al comune valore sugli estremi, in corrispondenza di tutti gli intervalli che si cancellano. La funzione così ottenuta è anche continua. Per farsi un'idea del grafico è opportuno immaginarla costruita per passi, esattamente come si fa con l'insieme C stesso.
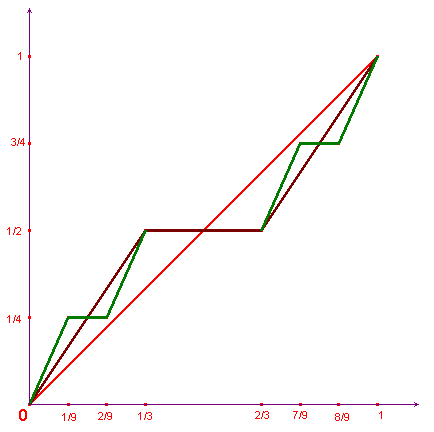
In sostanza, man mano che si procede nel raffinamento del
grafico si ottiene un sempre maggior numero di tratti
orizzontali, corrispondenti a tutti i segmenti che vengono
cancellati dall'intervallo [0,1], mentre la salita si
spezzetta in tratti sempre più corti, ma sempre
più verticali. La funzione vera e propria avrà
infiniti tratti orizzontali, che corrispondono alle
"pedate" della scalinata. La cosa
sorprendente è che se si calcola la lunghezza totale di
tutte le "pedate" si ottiene 1, cioè
tanto quanto lo spazio orizzontale complessivamente occupato
dalla scala stessa: non è facile intuire come faccia a
crescere da 0 ad 1 nonostante questo fatto!. Un'altra cosa
sorprendente è che, pur essendo crescente dal valore 0 al
valore 1, non risulta strettamente crescente su nessun
sottointervallo di [0,1]: basta ricordare le già note
proprietà dell'insieme di Cantor per capire che su
ogni sottointervallo di [0,1] ci sarà sempre un segmento
in cui la funzione risulta costante. Si noti inoltre che la
funzione è continua (per questo basta osservare che
è debolmente crescente e la sua immagine è un
intervallo), e quindi, pur essendoci infiniti gradini, non
c'è nessun salto del tipo: 
. Se la funzione non fosse continua, non ci sarebbe
alcuna meraviglia nel fatto che essa cresca da 0 ad 1, avendo
dei tratti orizzontali di lunghezza complessiva 1: basta
pensare, per esempio, alla funzione che vale 0 tra 0e 1/2, e 1
tra 1/2 ed 1. Veramente in questa funzione il diavolo ci ha
messo le corna!
E' anche interessante osservare che questa funzione è
derivabile quasi ovunque (tranne che sull'insieme
C, che ha misura nulla), con derivata nulla. Si ha
cioè f'(x)=0 
x di [0,1]\C, mentre f'(x) non
esiste sugli x di C. Se ora consideriamo una
funzione g(x) così definita: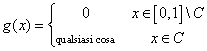 
, dove "qualsiasi cosa" è limitata,
possiamo notare che g(x) coincide quasi
ovunque con la derivata di f(x). La funzione
g(x) è sicuramente integrabile secondo Riemann
(teorema di Vitali-Lebesgue) e si ha 
. Se ne deduce che h(x)≠ f(x), per
x>0. In altri termini l'integrale della derivata
della scala diabolica (quando essa è derivabile!) non
è la scala diabolica. Ancora più diabolico!
Un'interessante idea, presa dall'ottimo sito sui frattali che si trova su library.thinkquest.org, per cercare di capire come è fatta questa funzione è di immaginare un Pacman (tipo quello dei videogiochi) che, partendo da sinistra, mangi progressivamente tutti i punti dell'insieme di Cantor, diventando via via più grosso ad ogni punto ingerito. Si può immaginare che parta da massa nulla e arrivi, alla fine del percorso, a massa 1. La funzione qui considerata si può pensare come la descrizione grafica dell'aumento di massa del Pacman.
Questa funzione oltre che con il nome di scala diabolica o scalinata del demonio, è anche nota con il nome di funzione di Vitali, dal matematico italiano Giuseppe Vitali, al cui contributo è dovuto, assieme a Lebesgue, il teorema fondamentale che caratterizza le funzioni integrabili secondo Riemann, sulla base della "numerosità" delle loro discontinuità.