Qualche "prodotto derivato"
Proponiamo in questa pagina una scelta tra i numerosi insiemi che si possono costruire a partire dall'insieme di Cantor.
1 - Il pettine di Cantor
Si tratta di fare l'unione degli insiemi ottenuti dai Cn che ci sono serviti per costruire l'insieme di Cantor, attribuendo loro una altezza fissa, e uguale per tutti, per ogni fissato n. Si ottiene un insieme che, limitatamente ai primi passi, ha l'aspetto seguente:

Si noti che, anche se all'apparenza il pettine che otteniamo è molto rado, in realtà i denti sono non solo infiniti, ma tanto infiniti quanto i punti dell'impugnatura del pettine!!
2 - Il quadrato di Cantor
Si ottiene con lo stesso procedimento utilizzato per l'insieme di Cantor, applicandolo però ad un quadrato, e cioè sopprimendo, successivamente, 1/3 dei segmenti su ciascuno dei due lati. L'insieme ottenuto è uguale a C×C. Nella figura qui sotto sono rappresentati i primi tre stadi del processo.

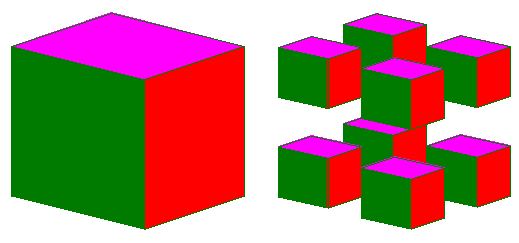
3 - Il cubo di Cantor
Si ottiene sempre con lo stesso processo, applicato però al cubo di lato 1. Nella figura qui sotto sono rappresentati i primi due passi nella costruzione di questo insieme.
4 - Le tendine di Cantor
Si tratta dell'insieme costruito visualizzando la applicazione dell'insieme di Cantor nell'intervallo [0,1], ottenuta rimpiazzando i "2" dei numeri dell'insieme di Cantor nella rappresentazione ternaria con degli "1" in rappresentazione binaria. Nella figura qui sotto sono rappresentati i primi tre passi nella costruzione di questo insieme.

5 - Gli anelli di Cantor
Questo insieme, ottenuto semplicemente per rotazione dell'insieme di Cantor attorno ad un estremo, può costituire un utile punto di partenza per costruire un modello matematico degli anelli di Saturno.

6 - Il villaggio di Cantor
La costruzione di questo insieme non richiede commenti. Chissà se Cantor, dopo tutte le vicissitudini passate, avrebbe il diritto di abitare nella casa più grande del suo villaggio, o se dovrebbe accontentarsi di una di quelle che si ottengono dopo molti passi nella costruzione!
