Polvere e trasformazioni geometriche
Un altro modo interessante per introdurre l'insieme di Cantor si basa su un opportuno uso delle trasformazioni geometriche e della tecnica dell'iterazione.
Consideriamo le due funzioni reali di variabile 
e 
. Si tratta di due funzioni
lineari, il cui grafico è una retta. Ci interessa la loro
restrizione all'intervallo [0,1] e in particolare
l'immagine di [0,1]. Nella figura qui sotto si controlla
immediatamente che l'immagine in questione è [0,1/3]
per la prima funzione e [2/3,1] per la seconda:
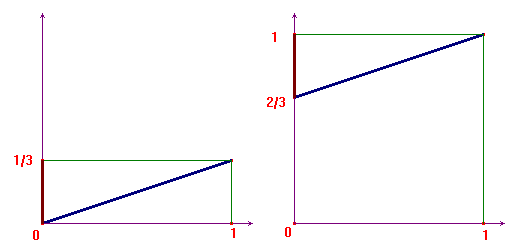
Dal punto di vista geometrico le due funzioni date possono essere considerate come due omotetie, con centro nei due estremi del segmento [0,1] e con rapporto di omotetia 1/3: si tratta di due contrazioni, cioè di due trasformazioni geometriche che trasformano una data figura in una in scala ridotta di un terzo.
Consideriamo ora la funzione, che indicheremo con
T=T1
T2, definita sui sottoinsiemi di
R e che ad ogni sottoinsieme A
R fa corrispondere l'insieme
T1(A)T2(A). Per quanto sopra osservato
abbiamo:
.
Se ora immaginiamo di applicare T a
C1, otterremo chiaramente l'insieme 
. Procedendo nello stesso modo, cioè
iterando il procedimento, otteniamo tutti gli insiemi
Cn, che abbiamo considerato per trovare
l'insieme di Cantor. L'insieme di Cantor C
può ora essere definito come l'unico sottoinsieme di
[0,1] che gode della proprietà che T(C)=C,
cioè che non viene mutato dalla trasformazione in
questione, o, come si dice che è invariante per
la trasformazione. Si usa dire che l'insieme di Cantor
è l'attrattore, in
R, della trasformazione T, con punto
di partenza [0,1].
Si tratta di un modo diverso di introdurre l'insieme di Cantor, molto importante nella costruzione dei frattali, in particolare con algoritmi automatici di calcolo. In un linguaggio di programmazione si tratta di progettare una funzione che operi la trasformazione T, e poi di applicarla successivamente, fornendo a T inizialmente l'intervallo [0,1] e poi il risultato stesso dell'applicazione di T.
La tecnica dell'iterazione è fondamentale nella programmazione e si incontra a tutti i livelli. Supponiamo per esempio di considerare la funzione per_due(x)=2x (cioè una funzione che, avuto in ingresso un numero, lo moltiplica per due). Se alla funzione comunichiamo il numero 1, essa restituisce 2; se questo risultato lo comunichiamo alla funzione stessa, essa restituisce 4, poi 8, ecc.: si otterranno le successive potenze di due. Se rappresentiamo la funzione come una scatola nera che, ricevuto in ingresso un numero, fornisce in uscita il doppio del numero, il procedimento si può rapprsentare con il seguente schema:
.
Risulta evidente il vantaggio di questa struttura: una volta che uno ha fatto la fatica di costruire la funzione "per_due", può utilizzarla, iterativamente, per ottenere le potenze di due. Anche se in questo caso la fatica di scrivere la funzione forse non è eccessiva, l'esempio illustra bene la potenza del metodo. E' evidente che il risultato dell'iterazione dipende da qual è il primo elemento fornito alla funzione: nel caso che stiamo trattando in questa pagina per ottenere l'insieme di Cantor dobbiamo fornire inizialmente alla funzione T l'intervallo [0,1].
Con la stessa tecnica possiamo ottenere il quadrato di Cantor: basterà che consideriamo quattro omotetie, con centri i quattro vertici del quadrato di lato 1, e rapporto 1/3; oppure il cubo di Cantor: basterà considerare otto omotetie con centri gli otto vertici del cubo di lato 1, e rapporto 1/3.
Per fornire un esempio più complesso consideriamo le seguenti quattro trasformazioni lineari di R2 in R2:
.
T2T3T4, costruito come sopra. Se proviamo ad
applicare ad esso lo stesso segmento [0,1] utilizzato per
l'insieme di Cantor, e iteriamo l'operazione
all'infinito, otteniamo il merletto
di Koch. Per capire che cosa esce si può
cominciare a costruire la prima iterazione, come rappresentato
graficamente qui sotto.
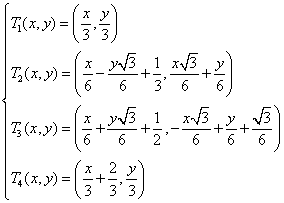E' allora immediato che la seconda iterazione darà la
figura seguente: 
.
Se si applica lo stesso operatore ad un triangolo equilatero si ottiene invece il fiocco di neve di von Kock.