Il pentagono regolare
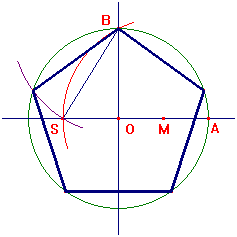
Tra le costruzioni più semplici consideriamo quella di Tolomeo: considerata la circonferenza di centro O e due diametri perpendicolari, con centro nel punto medio M di OA e apertura MB troviamo il punto S. BS è il lato del pentagono regolare (e OS quello del decagono).
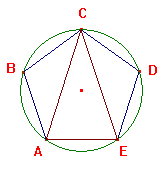
La costruzione di Euclide (Libro IV, Proposizione 11) si basa sull'osservazione che se ABCDE è il pentagono inscritto, nel triangolo isoscele ACE gli angoli alla base sono doppi di quello al vertice. Viene dunque costruito prima un triangolo siffatto (Libro IV, Proposizione 10), dopodiché si costruisce un triangolo inscritto ed equiangolo a questo, e infine il pentagono per bisezione dei due archi AC e CE minori di mezza circonferenza.
Una curiosità.
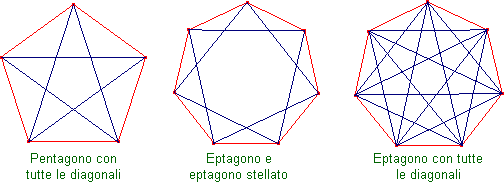
Il pentagono ha sempre suscitato notevoli interessi "extramatematici", forse in ragione del fatto che, tracciando tutte le sue diagonali, si ottiene il poligono stellato per "eccellenza": la stella a cinque punte. Come per tutti i poligoni stellati anche il pentagono si riproduce in fotocopia al suo interno, ma per il pentagono la figura risultante è chiaramente "meravigliosa", tanto che da molti è stata assunta come emblema (anche dai pitagorici). Nelle pratiche magiche la stella a cinque punte (considerata come l'unione di 3 -il maschio- e di 2 -la femmina) simboleggia energia, salute, luce...
Si vedano le figure qui sotto per capire la differenza che c'è tra un pentagono e, per esempio, un eptagono (i poligoni con un numero pari di lati sono meno interessanti da questo punto di vista, perché il poligono stellato non si traccia in unica soluzione, bisogna staccare la penna dal foglio).
Il pentagono e la geometria della carta piegata
Se prendete una sottile e lunga striscia rettangolare di carta e l'annodate, tirando bene le estremità e "spianando" successivamente il nodo, otterrete facilmente un pentagono regolare