Uno speciale triangolo isoscele
Dobbiamo costruire un triangolo isoscele in cui gli
angoli alla base siano doppi di quello al vertice. Seguiamo,
nelle linee essenziali, la costruzione di Euclide.
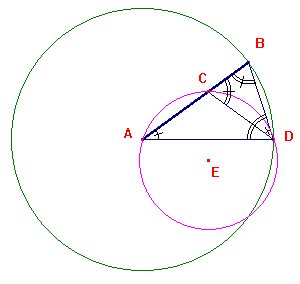
Dato un segmento AB, individuiamo la sezione aurea AC e costruiamo il
cerchio di centro A e raggio AB. Con centro in B e apertura
uguale ad AC individuiamo il punto D. Costruiamo la
circonferenza passante per A, C, D, con centro in E.
Poiché BD (=AC) è medio proporzionale tra BA e BH,
per il teorema della secante e della tangente, BD è
tangente al cerchio E. Ne segue che BAD=BDC, perché
insistono sullo stesso arco. L'angolo esterno BCD è
allora uguale a BDA (somma di angoli uguali) e quindi
all'angolo DBA (triangolo isoscele ADB). Si conclude che
BD=CD=AC e che ACD è isoscele. Allora ADB è doppio
di BAD.