Approssimazione delle funzioni mediante polinomi
Se una funzione f è derivabile in un punto c del suo dominio, essa ammette tangente in quel punto: ciò significa che la funzione può essere localmente approssimata con una retta. Si tratta di capire che cosa significa questa espressione.
Per chiarire le idee consideriamo il seguente esempio di funzione, volutamente patologico, il cui grafico è rappresentato a fianco in una scala speciale.
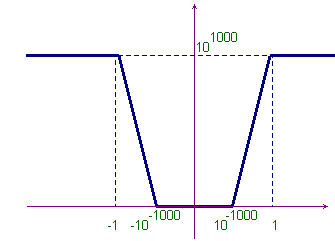
In realtà il segmento orizzontale sull'asse delle ascisse è così piccolo da non essere praticamente visibile, mentre la quota degli altri due segmenti orizzontali è così elevata da scomparire da ogni orizzonte. Ebbene questa funzione è approssimabile con l'asse delle ascisse in 0, ma ciò non ha palesemente alcuna utilità pratica. Questo esempio mostra chiaramente il significato dell'aggettivo locale, che si usa normalmente quando si ha a che fare con problemi di limite: interessa solo che la differenza tra la funzione e la sua tangente tenda a zero, quando l'incremento della variabile tende a zero. Naturalmente nei problemi pratici le cose non sono così complicate e l'approssimazione di una curva con la sua tangente ha una precisa valenza applicativa. Si pensi per esempio alla classica situazione astronomica: la terra descrive un'ellisse attorno al sole, ma, considerate le dimensioni di questa ellisse, il moto può essere considerato rettilineo per periodi di tempo non troppo lunghi, tanto che un sistema di riferimento solidale alla terra può essere considerato inerziale in prima approssimazione.
Sorge ora spontanea la domanda: esistono approssimazioni semplici migliori di quella data dalla retta tangente? In particolare: esistono approssimazioni mediante funzioni polinomiali? La risposta, affermativa per una vasta classe di funzioni, si può dedurre dai seguenti due teoremi, che enunciamo in ipotesi un po' più larghe di quelle minimali:
Formula di Taylor-Lagrange. Se una funzione f è derivabile n+1 volte in un intorno I di un punto c, per ogni x di I esiste un punto ξ compreso tra c e x tale che:
.
Se n=0 la formula coincide con quella contenuta nel teorema di Lagrange.
Formula di Taylor-Peano. Se una funzione
f è derivabile n-1 volte in un
intorno I di un punto c ed è derivabile
n volte in c, allora esiste una funzione
, definita in I e tendente a zero se
x tende a c, tale che, per ogni x
di I:
.
Il polinomio 
è detto n-esimo polinomio di Taylor o polinomio di Taylor di ordine n,
della funzione f in c ed è abitualmente
indicato con Tn,c(x). Il primo teorema
afferma in sostanza che se si approssima la funzione f
con il polinomio di Taylor si commette un errore
misurato da 
. Questo errore è
trascurabile se x è vicino a c
e anzi è dell'ordine di
(x-c)n+1. Nel secondo teorema
l'errore è misurato da 
,
e si possono ripetere le considerazioni già fatte, con la
sola differenza che nel primo si conosce una espressione
esplicita per l'errore, che rende possibili le stime della
grandezza dell'errore stesso, nel secondo caso no.
L'errore, nei due casi, si chiama anche Termine complementare, rispettivamente, di Taylor-Lagrange e di Taylor-Peano.
É sostanzialmente usando queste due formule che si riescono a calcolare valori approssimati delle funzioni di uso comune.
Le due formule, in particolare la seconda, sono molto usate anche nel calcolo dei limiti. Per una trattazione di questo problema si può consultare la pagina sull'uso della formula di Taylor.
Esempio
Data la funzione f(x)=sinx, calcolare il suo
polinomio di Taylor di ordine 5, relativo al punto 0. Si ha,
facilmente, 
. Tenendo conto delle
derivate, se si procedeva un passo oltre, si trovava, con una
migliore approssimazione: 
.
Queste formule possono essere usate per trovare valori
approssimati del seno, vicino all'origine. Se per esempio la
si usa per calcolare 
, che vale 0.5, si
trova 
, una ottima approssimazione, tenendo
anche conto che il valore 
non è molto
vicino a zero. L'espressione sopra riportata potrebbe anche
essere usata per valutare le dimensioni dell'errore.
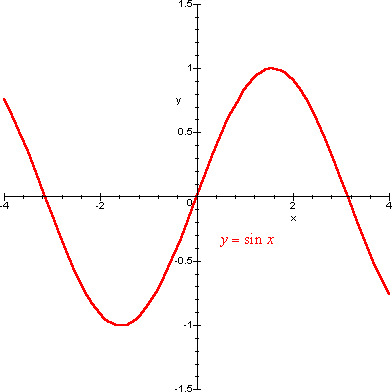
É interessante visualizzare graficamente il grado di approssimazione fornito dai vari polinomi di Taylor, all'aumentare dell'ordine. Si esamini la situazione qui di seguito, scegliendo dall'elenco quella desiderata.
- la sola funzione seno
- la funzione seno e il polinomio di ordine 1
- la funzione seno e il polinomio di ordine 3
- la funzione seno e il polinomio di ordine 5
- la funzione seno e i polinomi di ordine 1,3,5
Considerazioni più dettagliate sul significato di approssimazione polinomiale e in generale sui polinomi di Taylor si possono trovare in una monografia specifica sui polinomi di Taylor.