www.batmath.it di maddalena falanga e luciano battaia

www.batmath.it

Home page > Matematica > Calcolo differenziale > Derivabilità in intervalli

Funzioni derivabili in un intervallo

Teorema di Lagrange | Corollari | Teorema di Cauchy | Esercizi proposti

Una funzione f si dice derivabile in un intervallo, se è derivabile in ogni punto dell'intervallo. Se l'intervallo comprende uno o entrambi gli estremi, su di essi si considererà ovviamente solo la derivata sinistra o destra.

Teorema di Lagrange

Per le funzioni derivabili in un intervallo valgono alcuni risultati di grande importanza applicativa, che discendono essenzialmente dal famosissimo

Teorema di Lagrange (o del valor medio). Sia f una funzione definita e continua in un intervallo [a,b] chiuso e limitato, e derivabile almeno in ]a,b[. Allora esiste almeno un punto c di ]a,b[ tale che

Nulla cambia se l'intervallo è [b,a], anziché [a,b].

Dimostrazione

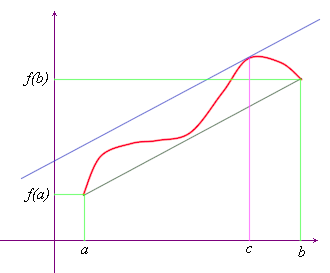
Questo teorema ha una ovvia e immediata interpretazione grafica. Data una funzione con le caratteristiche indicate, esiste almeno un punto c interno all'intervallo di definizione dove la tangente al grafico è parallela alla retta passante per gli estremi (a,f(a)) e (b,f(b)).

Come mostra la figura qui sotto, in realtà di tali punti c ce ne possono essere anche più d'uno.

teorema di Lagrange

É utile rendersi anche conto del perché il teorema prende il nome di Teorema del valor medio. Si può utilizzare il seguente ragionamento: se f(t) rappresenta la distanza percorsa da un corpo al variare del tempo, rappresenta la velocità media nell'intervallo di tempo [a,b]. Il teorema di Lagrange afferma che ci deve essere almeno un istante in cui la velocità istantanea (f'(t)) è uguale alla velocità media.

Se per caso f è tale che f(b)=f(a), si deduce che in c si ha f'(c)=0. Questo caso particolare è noto come Teorema di Rolle e fu dimostrato prima di quello di Lagrange. Se si ricontrolla la dimostrazione del teorema di Lagrange, si vede subito che essa utilizza proprio una funzione ausiliaria che assume valori uguali agli estremi. Si può vedere anche una dimostrazione grafica di come si possa passare dal caso particolare (Rolle) al caso generale (Lagrange).

Le ipotesi di continuità in [a,b] e derivabilità almeno in ]a,b[ sono essenziali per la validità del teorema, come mostrano i due esempi qui sotto che proponiamo senza commenti, invitando il lettore a trovare rappresentazioni analitiche di funzioni con le caratteristiche di quelle proposte.

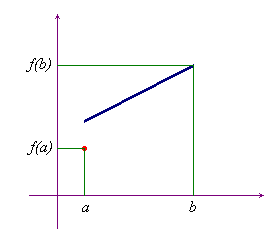
grafico

Una funzione continua e derivabile solo in ]a,b[.

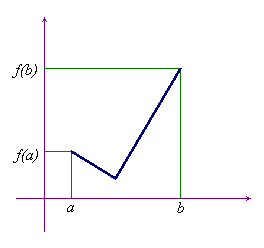
grafico

Una funzione continua in [a,b] ma non derivabile in tutto ]a,b[.

Per il caso particolare di Rolle è, ovviamente, indispensabile la condizione f(a)=f(b): per un controesempio si può pensare alla funzione f(x)=x nell'intervallo [0,1].

Proponiamo qualche esercizio applicativo.

Esercizio 1. Data la funzione determinare i punti dell'intervallo [0,4] che soddisfano la condizione espressa dal teorema di Lagrange.

Essendo , ed essendo la funzione continua in [0,4] e derivabile in ]0,4], basterà risolvere l'equazione, nell'incognita c, : il teorema di Lagrange ci assicura che ci deve essere almeno una soluzione. Si trova facilmente c=1. Si noti che la funzione non è derivabile in 0.

Esercizio 2. Si consideri la funzione 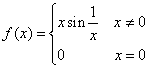. Si provi, usando il teorema di Rolle, che esistono infiniti punti dell'intervallo [0,1/π] dove la derivata si annulla.

La funzione data è continua nell'intervallo assegnato e derivabile tranne che per x=0 (che è un estremo dell'intervallo e quindi non crea problemi). Inoltre la funzione assume valori uguali agli estremi (in quanto vale zero), quindi almeno un punto con le caratteristiche richieste esiste. Per provare che ce ne sono infiniti, basta ripetere il ragionamento applicando il teorema sui sottointervalli del tipo .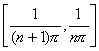

Esercizio 3. Si consideri un arco di parabola y=ax²+bx+c, compreso tra due punti P e Q di ascissa p e q. Si dimostri che la corda PQ è parallela alla tangente condotta per il punto di ascissa m=(p+q)/2.

Il teorema di Lagrange applicato all'intervallo [p,q] afferma che esiste almeno un punto, m, interno all'intervallo [p,q], tale che

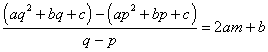. Basta semplificare per concludere.

I famosi corollari

Non è forse azzardato affermare che il teorema di Lagrange gode di maggior fama per merito dei suoi corollari che non per se stesso. Li enunciamo tutti tre.

Corollario 1. Se una funzione è derivabile con derivata nulla su un intervallo, allora è costante.

Corollario 2. Se due funzioni hanno la stessa derivata in un intervallo, esse differiscono per una costante.

Corollario 3. Se una funzione ha derivata maggiore di zero in un intervallo, è strettamente crescente nell'intervallo, se ha derivata minore di zero è strettamente decrescente.

Il terzo corollario fornisce lo strumento essenziale per rappresentare i grafici delle funzioni derivabili: trovata la derivata di una data funzione, si tratta di determinarne il segno per concludere dove la funzione cresce e dove decresce e quindi anche quali sono gli eventuali massimi e minimi locali.

Si osservi che il terzo corollario ha come conseguenza banale che se un funzione (derivabile) è crescente in ogni punto di un intervallo, è crescente nell'intervallo: la cosa sarebbe vera anche per funzioni non necessariamente derivabili (lo si provi per esercizio), ma è in ogni caso essenziale che l'insieme in cui si considera la funzione sia un intervallo. Basta pensare alla funzione f(x)=tgx che ha ovunque derivata positiva (cioè è crescente in ogni punto del dominio), ma non è crescente su tutto il dominio.

Esempio 1. Trovare i massimi e minimi locali della funzione f(x) = x³-3x+7.
Poiché f'(x) = 3x²-3, si conclude che la funzione è crescente per x<-1 e per x>1, mentre è decrescente tra -1 e 1. Avrà dunque un massimo locale per x=-1 (di valore 11) e un minimo locale per x=1 (di valore 5).

Esempio 2. Provare che la funzione f(x)=ln(1+x³) è invertibile in tutto il suo dominio, dire se la inversa è derivabile per x=0 e per x=ln2 e, in caso affermativo, calcolare la derivata dell'inversa.
La derivata della funzione è f'(x)=3x²/(1+x³). Se ne deduce che la funzione cresce in tutto il suo dominio. I punti 0 e ln2 nel dominio dell'inversa corrispondono ai punti 0 e 1 nel dominio di f. Poiché f'(0)=0, mentre f'(1)=3/2, se ne deduce che l'inversa non è derivabile in 0, mentre è derivabile in ln2 e si ha

Il teorema di Cauchy

Una generalizzazione del teorema di Lagrange (che dunque comprenderà il teorema di Lagrange stesso come caso particolare) è costituita dal seguente

Teorema di Cauchy. Siano f e g due funzioni continue in un intervallo [a,b] e derivabili almeno in ]a,b[. Sia inoltre g'(x)≠0. Allora esiste almeno un punto c di ]a,b[ tale che

É immediato che, se g(x)=x, da questo teorema si deduce quello di Lagrange e quindi che sarebbe utile dimostrare solo questo teorema più generale. Inoltre questo teorema è molto importante e viene utilizzato per la dimostrazione di altri risultati fondamentali del calcolo differenziale (esempio i teoremi di l'Hôpital). In realtà nelle applicazioni allo studio di funzioni (a cui siamo maggiormente interessati) quelli che contano sono i corollari del teorema di Lagrange ed è per questo che abitualmente si focalizza l'attenzione su di essi.