La funzione valore assoluto
La disequazione con valori assoluti
Se in una disequazione la variabile compare sotto valore assoluto conviene, utilizzando la definizione di valore assoluto, distinguere i vari casi che si possono presentare e risolvere le diverse disequazioni ottenute: la presenza di valori assoluti non richiede quindi l'introduzione di alcuna nuova tecnica risolutiva per le disequazioni.
Chiariamo il metodo con alcuni esempi.
Esempio 1. Risolvere la disequazione x +
|x2-1| < 0.
Poiché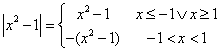 
, si devono considerare
due casi:
-
x ≤ -1
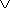x ≥ 1. La disequazione diventa:
x + (x2-1) < 0.
La soluzione è immediata: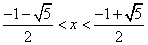
. Tenendo conto delle condizioni (x ≤
-1 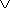x ≥ 1), si
trova: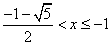 
.
-
-1 < x < 1. La disequazione
diventa: x - (x2-1) < 0, ovvero
x2 -x -1 > 0. Anche la soluzione
è immediata:
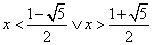. Tenendo conto
delle condizioni (-1 < x < 1), si trova
facilmente: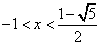 
.
In conclusione, facendo l'unione dei
risultati trovati nei due casi, si ottiene: 
.
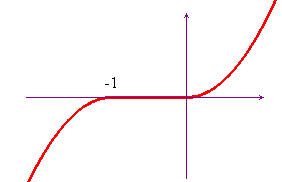
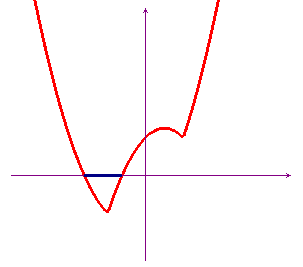
Il grafico qui sotto, dove è rappresentata la
funzione
f(x) = x + |x2-1|, conferma il risultato
trovato.
Esempio 2. Risolvere la disequazione: |x+1| + |2-x| + x - 6 > 0. Si deve esaminare il segno di ciascuno degli argomenti dei valori assoluti presenti nel testo. I risultati si possono riportare in un grafico del tipo +/-, anche se qui non si deve poi eseguire alcun prodotto. Si trova:
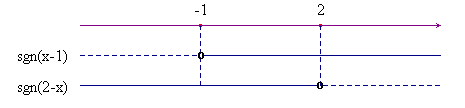
Se ne deduce che si devono distinguere tre casi:
-
x < -1. Poiché per questi valori
|x+1| = -(x+1), mentre |2-x| = (2-x), la
disequazione data si può scrivere:
-(x+1)+(2-x)+x-6>0. La soluzione è: x < -5. -
-1 ≤ x < 2. (Si noti che,
conformemente alla convenzione in uso, abbiamo considerato il
segno di "=" accanto a quello di
">"). In questo caso |x+1| =
(x+1), e |2-x| = (2-x), per cui la disequazione
data si può scrivere:
(x+1)+(2-x)+x-6>0. Tenendo conto delle condizioni, non si trova alcuna soluzione. -
x ≥ 2. In questo caso |x+1| =
(x+1), mentre |2-x| = -(2-x), per cui la
disequazione data si può scrivere:
(x+1)-(2-x)+x-6>0. La soluzione è: x > 7/3.
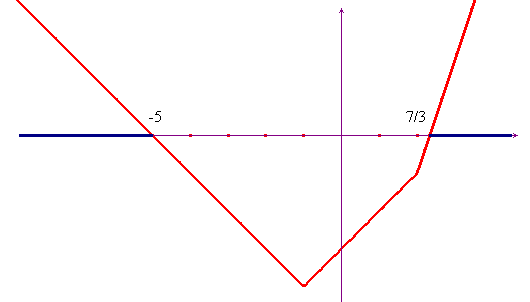
Facendo l'unione dei risultati si trova l'insieme di soluzioni S = x <-5 x > 7/3.
Anche in questo caso la rappresentazione grafica della funzione
a primo membro, 
, conferma il
risultato trovato.
Esempio 3. Risolvere la disequazione: 
. Esaminando prima il segno dell'argomento del
valore assoluto "più interno" si conclude che
si devono distinguere due casi:
-
x < -2. La disequazione si riduce a
|1-(-(x+2))|+x-1≤0, ovvero
|x+3|+x-1≤0. Si devono distinguere di
nuovo due casi:
- x < -3. La disequazione si riduce a -4≤0 che è sempre vera.
- -3 ≤ x < -2. La disequazione si riduce a 2x+2≤0, che, nell'intervallo in questione, è sempre vera.
-
x ≥ -2. La disequazione si riduce a
|1-(x+2)|+x-1≤0, ovvero
|-x-1|+x-1≤0. Si devono distinguere di
nuovo due casi:
- -2 ≤ x < -1. La disequazione si riduce a -2≤0, che è sempre vera
- x ≥ -1. La disequazione si riduce a -(-x-1)+x-1≤0, che, tenendo conto della condizione x≥-1, risulta verificata per -1 ≤ x ≤ 0.
Facendo la riunione dei risultati trovati si conclude che l'insieme delle soluzioni è x ≤ 0.
In questo caso il grafico della funzione a primo membro, 
, non solo conferma il risultato trovato, ma
mostra anche come sarebbe stato immediato trovarlo, senza alcun
calcolo!
Consigliamo di usare sempre una
calcolatrice adatta per tracciare i grafici coinvolti nelle
disequazioni. Anche se di solito da essi non si possono dedurre
le soluzioni nella forma richiesta negli esercizi
(principalmente per la difficoltà nel valutare
graficamente le ascisse dei punti di intersezione tra i grafici
o tra un grafico e l'asse delle ascisse), si può in
ogni caso avere un buon controllo dei risultati trovati.
Il segno di una funzione contenente valori assoluti
Per ottenere il segno di una funzione contenente valori assoluti si può procedere con la tecnica generale indicata. Occorre prestare molta attenzione al fatto che, una volta trovato il dominio e l'insieme dove f(x) > 0, non è sempre agevole concludere immediatamente: come per le funzioni irrazionali, anche per questo tipo di funzioni (a differenza di quello che succede con i polinomi) l'insieme dei punti dove f(x)=0 può essere molto complesso e non essere costituito da punti isolati. Anche in questo caso una rappresentazione grafica può essere di grande aiuto. Chiariamo il fatto con alcuni esempi.
Esempio 1. Trovare il segno di 
. Il grafico a fianco mostra subito che la funzione:
- non è definita per x = 0;
- è positiva per x > 0;
- è negativa per x < 0.
La funzione passa dunque da valori positivi a negativi senza annullarsi. Il risultato si poteva trovare anche, facilmente, per via algebrica.
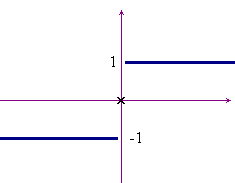
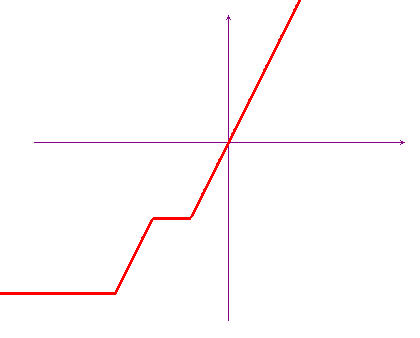
Esempio 2. Trovare il segno di 
. Il grafico di seguito mostra che:
- f(x) > 0 per x > 0;
- f(x) < 0 per x < -1;
- f(x) = 0 per -1 ≤ x ≤ 0.
La funzione si annulla quindi in un intero intervallo, anziché in punti isolati come succede per i polinomi (che hanno al massimo tanti zeri reali quant'è il loro grado).
