La funzione valore assoluto
La funzione valore assoluto ha grande importanza in tutte le applicazioni, importanza confermata anche dal fatto che tutte le calcolatrici tascabili la implementano con un apposito tasto.
La funzione,
indicata con \(f(x)=\mathrm{abs}(x)=|x|\), è così
definita \[|x|=\sqrt{x^2}=\left\{\begin{array}{rl}x&x\geq
0\\-x&x<0\end{array}\right.\;.\]
La scrittura |x| si legge "modulo di x". Si tratta di una funzione che accetta in ingresso numeri reali restituendo, in uscita, lo stesso numero se positivo (o nullo), l'opposto se negativo. Per numeri positivi la funzione coincide dunque con la funzione identità di R in R. Dal punto di vista teorico, essendo definita come la composta tra la funzione estrazione di radice quadrata e la funzione elevamento al quadrato (che non sono una l'inversa dell'altra) non ci sarebbe bisogno di un capitolo speciale per trattarla; il capitolo si rende però indispensabile per il suo continuo uso nelle applicazioni. Per una trattazione completa dei problemi connessi con l'elevamento al quadrato e l'estrazione di radice, puoi vedere la pagina sulla radice quadrata. Si noti che avremmo anche potuto scrivere \[|x|=\left\{\begin{array}{rl}x&x > 0\\-x&x\leq 0\end{array}\right.\] o, addirittura, \[|x|=\left\{\begin{array}{rl}x&x \geq 0\\-x&x\leq 0\end{array}\right.\,.\] Per tradizione si usa però mettere il segno di "=" assieme a quello di maggiore, invece che a quello di minore.
Dal punto di vista grafico questa funzione ha una importantissimo significato. Data la retta reale, su cui si sia stabilito un sistema di ascisse, il valore assoluto, o modulo, di un numero reale x, rappresenta la distanza di x dall'origine.
Questo significato geometrico diventa particolarmente importante quando si estende questa funzione ai numeri complessi, dove la funzione modulo è proprio definita come la distanza del punto P, rappresentativo del numero complesso z nel piano di Gauss, dall'origine.
Per completezza riportiamo anche il grafico di questa funzione e la costruzione, anche con un'animazione CabriJava.
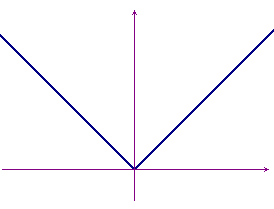
Nelle espressioni in cui compare il valore assoluto è spesso (ma non sempre!) conveniente considerare i vari casi che si possono presentare, a seconda del segno dell'espressione che compare sotto valore assoluto (espressone che chiameremo argomento del valore assoluto). Chiariamo questo fatto con qualche esempio.
Esempio1. La funzione \(f(x)=x+|x|\) si può scrivere anche così: \[f(x)=x+|x|= \left\{\begin{array}{rl}2x&x\geq 0\\0&x<0\end{array}\right.\;,\] e quest'ultima scrittura rende immediato, per esempio, tracciare il grafico, costituito da due semirette.
Esempio 2. La funzione \(f(x)=x^2-x+|x-1|\) f(x) = x2-x+|x-1| si può anche scrivere così: \[f(x)=x^2-x+|x-1|=\left\{\begin{array}{ll}x^2-1&x\geq 1\\x^2-2x+1&x<1\end{array}\right.\;,\] e anche ora questa scrittura rende evidente il fatto che la nostra funzione è costituita da due rami di parabola.
Per
evitare facili errori nei segni si può utilizzare la
seguente "regola": considerata una
espressione "racchiusa tra le barre del valore
assoluto", si esamina il segno dell'espressione;
nell'insieme ove essa è positiva le barre del valore
assoluto possono essere sostituite da una normale parentesi,
nell'insieme dove è negativa le barre devono sempre
essere sostituite da una normale parentesi, cambiando
però il segno a tutti i termini nell'interno.
Riprendendo in esame l'esempio 2 appena considerato si ha:
\(x^2-x+|x-1|=x^2-x+(x-1)\) oppure \(x^2-x+(-x+1)\), a seconda
che il termine \(x-1\) sia positivo o negativo.
Dal punto di vista dell'analisi è da segnalare il fatto che questa funzione, essendo la composta di due funzioni continue, è continua, mentre non risulta derivabile (ha un punto angoloso nell'origine), ed in effetti la funzione radice quadrata (cioè una delle sue due componenti) non è derivabile nell'origine (ha tangente verticale).
Puoi vedere ulteriori esempi e discussioni, in particolare coinvolgenti la risoluzione di disequazioni con valori assoluti.