www.batmath.it

Funzioni irrazionali

Si chiamano irrazionali quelle funzioni in cui la variabile figura sotto il segno di radice. Per esempio è irrazionale , non è irrazionale (si tratta di un binomio di primo grado!).

É importante mettere subito in evidenza il fatto che non esistono regole generali per risolvere le disequazioni irrazionali o per trovare il segno di funzioni irrazionali. A nostro avviso non conviene imparare le "regole" che sono proposte in molti testi, in quanto si riferiscono solo ad alcuni casi particolari e si dimenticano quasi subito (supposto che qualcuno abbia avuto voglia di impararle!).

Le disequazioni irrazionali - risoluzione per via algebrica

La risoluzione per via algebrica si basa sull'idea di trasformare la disequazione irrazionale in un'altra, ad essa equivalente, in cui la variabile non compaia più sotto radice. Per fare questo occorre elevare ambo i membri della disequazione ad una opportuna potenza. Purtroppo però, come già osservato, l'elevazione a potenza (in particolare ad una potenza pari) non è di solito lecita. Inoltre l'elevazione a potenza può complicare il problema anzichè semplificarlo. Consideriamo per esempio la disequazione: . Se, dopo aver trovato il dominio (x≥0), elevo al quadrato (trascurando -per il momento- i problemi connessi con questa operazione) ottengo:  , che è più complessa della precedente e in cui la variabile compare ancora sotto radice. Se invece trasformo la disequazione in e poi elevo al quadrato (anche qui trascurando -per il momento- i problemi connessi con questa operazione), ottengo , che è di secondo grado e quindi di facile risoluzione. Si deve quindi procedere con la massima cautela, valutando accuratamente le varie possibilità .

Consigliamo di procedere nel seguente modo:

Alcuni esempi chiariranno il metodo da seguire.

Esempio 1. Risolvere la disequazione .

• Dominio: x ≤ 2 x ≥ 7.
• É chiaro che non conviene elevare al quadrato direttamente (comparirebbero tre radicali al posto di uno!). Se riscriviamo la disequazione nella forma: 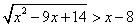, una elevazione al quadrato trasforma la disequazione in una di secondo grado di immediata risoluzione.
• Consideriamo dunque la disequazione 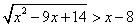. Il primo membro, quando ha senso, è sempre positivo, il secondo membro può essere positivo o negativo: se positivo (o nullo) si elevano al quadrato ambo i membri, se negativo la disequazione è certamente vera. Si dovranno allora distinguere due casi:
  • x - 8 ≥ 0, cioè x ≥ 8. Elevando al quadrato e semplificando e risolvendo si ottiene: 7x-50>0. Si può dunque considerare il sistema: 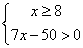, la cui soluzione è:  x ≥ 8.
  • x - 8 < 0, cioè x<8. In questo caso il primo membro (positivo) è sicuramente maggiore del secondo (negativo), per cui la disequazione è sicuramente verificata (per gli x del dominio!!).

Si conclude che l'insieme delle soluzioni è: S =  ]-∞,2] [7,+∞[, o, equivalentemente, x ≤ 2 x ≥ 7.

Esempio 2. Risolvere la disequazione .

• Dominio: x ≤ 3/2.
• Chiaramente non conviene elevare al quadrato direttamente. Si può trasformare in 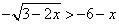oppure in 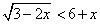. La seconda forma è chiaramente preferibile in vista dell'elevazione al quadrato perché, in essa, il primo membro è sempre positivo.
• Consideriamo dunque la disequazione 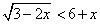. Il primo membro, quando ha senso, è sempre positivo, il secondo può essere positivo o negativo. Se positivo (o nullo) si può elevare al quadrato, se negativo la disequazione non ha sicuramente soluzioni (un numero positivo non può essere minore di uno negativo!). Si può dunque considerare un unico caso:
  • 6 + x ≥ 0, cioè x ≥ -6. Elevando al quadrato e semplificando si ottiene 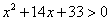. Si può considerare il sistema: 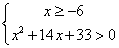, che ha come soluzioni x > -3. Ad essere assolutamente pignoli bisognerebbe tenere conto che per x ≥ 3/2 la disequazione non ha senso (dominio!), e in effetti alcuni testi tengono ripetutamente conto di questo fatto nel risolvere una disequazione irrazionale. Riteniamo che sia solo una perdita di tempo: l'importante è tenerne conto al momento giusto!.

Tenendo conto del dominio si trova l'insieme di soluzioni S =  ]-3 , 3/2], ovvero -3 < x ≤ 3/2.

Esempio 3. Risolvere la disequazione .

• Dominio. Le condizioni da imporre sono: 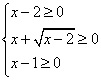. Per risolvere questo sistema, anziché partire subito con i calcoli conviene osservare che dalla prima si ottiene x ≥ 2, dopodiché la seconda è la somma di due positivi e la terza è sicuramente vera: la soluzione è x ≥ 2. 
  Spesso nel risolvere una disequazione o un sistema si possono ridurre notevolmente i tempi come abbiamo fatto qui: conviene perdere qualche secondo per valutare l'esercizio nel suo complesso, prima di partire come un bulldozer, e questo consiglio non vale solo per le disequazioni!
• Quando i due membri hanno senso essi sono positivi e la forma proposta è la migliore per elevare al quadrato.
• Quadrando e semplificando si ottiene: 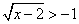. Questa disequazione è sempre verificata, per cui la soluzione finale è x ≥ 2. 

Esempio 4. Risolvere la disequazione .

• Dominio: x ≥ 3.
• In qualunque forma si scriva la disequazione un'elevazione al quadrato non elimina i due radicali, ma in ogni caso dopo un'elevazione al quadrato ne rimane uno solo. Si può però osservare che nella forma assegnata il primo membro può essere sia positivo che negativo e, in ogni caso, che nel doppio prodotto compaiono termini di secondo grado (sotto la radice residua!). Se si scrive invece nella forma 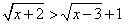,  i due membri, quando hanno senso, sono positivi e, nell'elevazione al quadrato, non compaiono termini di secondo grado. É questa la forma da preferire.
• Considerata dunque la disequazione 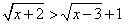, quadrando e semplificando si ottiene: 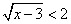, che ha come soluzioni x < 7.

Tenendo conto del dominio trovato si conclude che l'insieme di soluzioni è: S = [3,7[, ovvero 3 ≤ x < 7.

Esempio 5. Risolvere la disequazione . In questo caso non ci sono problemi né con il dominio né con l'elevazione al cubo (sempre possibile). Si ottiene facilmente: -x³ - x + 2 ≥ 0. Scomponendo in fattori si ottiene , il cui insieme di soluzioni è S = ]-∞,1], ovvero x ≤ 1.

Le disequazioni irrazionali - risoluzione grafica

Per le disequazioni irrazionali la risoluzione per via grafica è particolarmente utile, sia come metodo proprio sia per controllare i risultati ottenuti per via algebrica (dove è molto facile sbagliare qualche calcolo!) per la semplicità con cui possono essere ottenuti grafici anche complessi utilizzando i computer o semplici calcolatrici tascabili.

Se riprendiamo in esame la disequazione sopra considerata , e tracciamo il grafico della funzione a primo membro, con un qualunque programma (Derive™, Maple™, Mathematica™, o addirittura l'onnipresente Cabri, come abbiamo fatto noi), possiamo immediatamente controllare la bontà del risultato che abbiamo ottenuto per via algebrica. In questo caso il grafico ci fornisce anche immediatamente le soluzioni, senza alcun ulteriore calcolo.

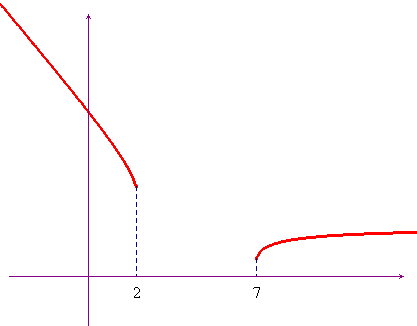
Se volessimo essere pignoli e ottenere il grafico con i tradizionali metodi dell'analisi non ci sarebbe alcuna difficoltà. Questo stesso risultato può però essere ottenuto per via grafica anche con metodi più "elementari", con le seguenti considerazioni. 

Riscritta la disequazione nella forma , e considerate le funzioni che stanno a primo e secondo membro, possiamo risolvere la disequazione esaminando il seguente sistema: : si tratta di trovare i valori di x per cui il primo grafico sta sopra il secondo. Il secondo grafico è una retta, tracciabile per via elementare. Il primo può essere tracciato utilizzando la teoria delle coniche. Infatti da possiamo ottenere il seguente sistema   o, meglio, . La seconda equazione rappresenta una conica di cui dobbiamo prendere solo la parte compresa nel primo e secondo quadrante (y≥0). Si ottiene il grafico finale riportato qui sotto, da cui, naturalmente, si traggono sempre le stesse conclusioni.

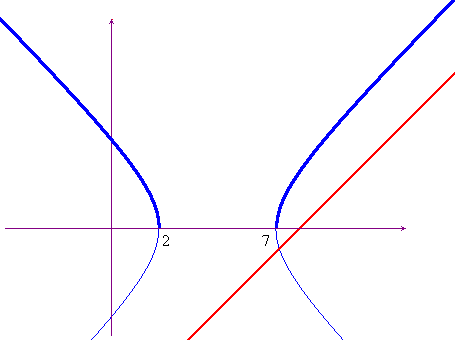
Il grafico in blu rappresenta la conica, quello in rosso la retta. Naturalmente, come più sopra accennato, della conica abbiamo considerato solo la parte nel primo e secondo quadrante.

La tecnica "elementare" qui utilizzata può essere applicata a tutte le disequazioni irrazionali del tipo , se f e g sono polinomi al massimo di secondo grado. Nel caso che g sia di primo grado le intersezioni tra le due curve possono anche essere trovate analiticamente (intersezioni tra una conica e una retta), se invece g è di secondo grado non è detto che le intersezioni possano essere trovate analiticamente (intersezioni tra una conica e una parabola): in ogni caso la rappresentazione grafica fornisce importanti informazioni sulle soluzioni della disequazione.

Consideriamo, per chiarire le idee, un altro esempio. Si debba risolvere la seguente disequazione: . Procedendo come nell'esempio precedente otteniamo il sistema: 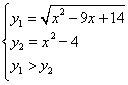. Il primo grafico è lo stesso di prima, mentre il secondo è una parabola: si tratta di trovare i punti per cui l'iperbole "sta sopra" la parabola. 

Sempre con Cabri abbiamo ottenuto i grafici qui sotto. Se ne deduce facilmente che la disequazione è verificata per  α < x < 2. Per determinare il valore di α dovremmo trovare le radici del polinomio che si ottiene quadrando ambo i membri dell'equazione , e cioè del polinomio di quarto grado: . Purtroppo solo radice x=2 è razionale mentre le altre tre no. Di queste ci interessa solo α, perché le altre due stanno nella parte di iperbole che non fa parte del nostro grafico. 

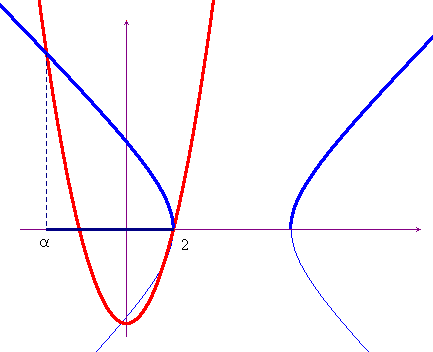
Anche il grafico qui sotto, ottenibile con le usuali tecniche dell'analisi o, molto più velocemente, con uno dei programmi di grafica indicati sopra, consente di trarre le stesse conclusioni. Da entrambi i grafici si può ottenere anche una stima del valore di α, che risulta essere compreso tra -4 e -3. Stime più precise si possono ottenere zoomando sui grafici o con le usuali tecniche dell'analisi numerica. In ogni caso la tecnica grafica fornisce preziosi indicazioni di prima approssimazione, senza molta fatica.

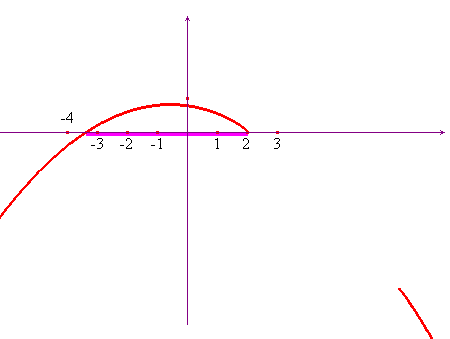
Il segno di una funzione irrazionale

Per ottenere il segno di una funzione irrazionale si può procedere con la tecnica generale indicata. Occorre prestare molta attenzione al fatto che, una volta trovato il dominio e l'insieme dove f(x) > 0, non è sempre agevole concludere immediatamente: per questo tipo di funzioni (a differenza di quello che succede con i polinomi) l'insieme dei punti dove f(x)=0 può essere molto complesso e non essere costituito da punti isolati. Anche in questo caso una rappresentazione grafica può essere di grande aiuto. Chiariamo il fatto con alcuni esempi.

Esempio 1. 
Determinare il segno di:  . Il grafico di seguito mostra subito che 

• f(x) > 0 per x < -1 x > 1;
• f(x) = 0 per -1 ≤ x ≤ 1;
• f(x) < 0 per nessun valore di x.

Si provi a risolvere il problema per via algebrica per un utile confronto.

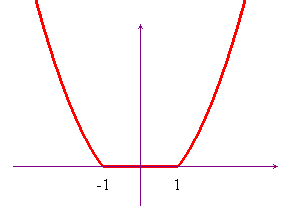
Esempio 2. 
Determinare il segno di:  . Il grafico di seguito mostra subito che 

• f(x) > 0 per x > o;
• f(x) = 0 per -1 ≤ x ≤ 0;
• f(x) < 0 per x ≤ -1.

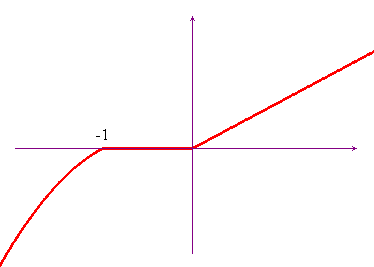
Se non si conosce la funzione valore assoluto è meglio evitare di tentare la soluzione di questo problema per via algebrica!.

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 02/09/2002 - ultimo aggiornamento il 01/09/2003