La curva di von Koch
"Un filo sottilissimo comunque disposto su di un piano, il segno tracciato dalla punta di una matita che si fa scorrere su di un foglio, il contorno di una superficie piana, ci danno l'idea di ciò che chiamiamo linea piana".
Si tratta dell'introduzione al concetto di curva preso da un comune testo di geometria. É in effetti in questi termini che abitualmente pensiamo ad una curva.
In
realtà il concetto di curva è molto complesso e
qui vogliamo far vedere su qualche esempio come le
"definizioni" sopra riportate vadano "prese con
le pinze".
(Per comprendere appieno quanto diremo è opportuno fare riferimento al noto processo che porta alla rettificazione della circonferenza.)
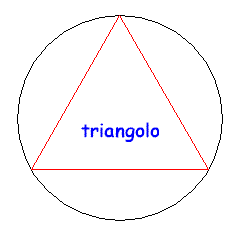
Esaminiamo ora il triangolo equilatero inscritto in un
circonferenza, e supponiamo, per semplicità, che esso
abbia lato 1. (Basterà quindi che il raggio della
circonferenza sia 
).
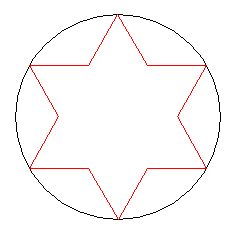
Se dividiamo ciascuno dei tre lati in tre parti uguali, togliamo
la parte centrale e la sostituiamo con i due lati di un
triangolo equilatero di lato 
,
otteniamo una figura come quella qui di seguito riportata,
comprendente dodici lati tutti di lunghezza .
Ogni lato del triangolo equilatero di partenza è
sostituito da quattro segmenti di lunghezza 
:
la figura avrà come contorno una spezzata di 3× 4
lati, con un perimetro lungo 
.
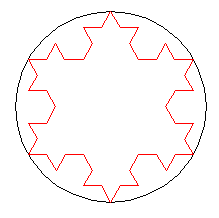
Se ripetiamo il procedimento su ciascuno dei dodici lati della
figura sopra riportata, avremo una figura come quella qui di
seguito, con 48 lati di lunghezza 
.
Infatti ogni lato della figura precedente viene sostituito da 4
lati, ciascuno con lunghezza
del precedente.
Il perimetro della figura sarà ora 
.
Si può a questo punto osservare che il perimetro del
triangolo di partenza si può scrivere nella forma 
, mentre quello della penultima figura si
può scrivere nella forma 
.
Non è difficile convincersi che, dopo aver ripetuto n
volte il procedimento, il perimetro della figura sarà:
.
Se per esempio n=100, si ottiene 
; se la misura originale era in metri si tratta
all'incirca di 10.000.000.000 (dieci miliardi) di
chilometri!!.
La curva che si ottiene come limite per n tendente
all'infinito ha una singolare proprietà: ha infatti
una lunghezza infinita, ma racchiude un'area finita, come
mostra il fatto che la regione ottenuta è contenuta
all'interno della circonferenza in cui era inscritto il
triangolo equilatero da cui siamo partiti per la nostra
costruzione.
È chiaro che già quando abbiamo ripetuto il procedimento cento volte la figura non è più disegnabile tecnicamente sul foglio (dovremmo disegnare circa 1060 lati, ognuno lungo circa 10-48 metri!), ma il "disegno" può essere fatto almeno dal punto di vista teorico. Le matite che la nostra mente può concepire possono fare un simile disegno: muovendosi alla velocità della luce la nostra matita mentale impiegherebbe solo circa dieci ore per percorrere tutto il contorno!. La curva limite richiede invece un livello di astrazione molto maggiore: anche muovendosi alla velocità della luce la nostra matita mentale non riuscirebbe mai a disegnare tutto il contorno, in quanto avrebbe bisogno di un tempo infinito.
Non è difficile calcolare l'area racchiusa dalla
curva limite, area che risulterà finita, come già
detto. Indichiamo con A l'area del triangolo equilatero di
partenza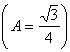 
; con il primo passo si
aggiungono tre triangoli, ciascuno con area 
;
con il secondo passo si aggiungono 3·4 triangoli,
ciascuno con area 
; con l'ennesimo passo
si aggiungeranno 
triangoli, ognuno con area 
. L'area, dopo n passi sarà:
Raccogliendo, semplificando, e tenendo conto della formula per la somma di una progressione geometrica si ottiene:
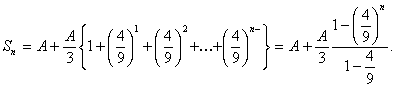
Se facciamo tendere n all'infinito si ottiene immediatamente
. Come era prevedibile l'area della
regione ottenuta è di poco più grande di quella
del triangolo di partenza.
Questa curva limite è stata essenzialmente proposta dal matematico tedesco Helge von Koch nel 1904 ed ha un'altra interessante proprietà: non ammette tangente in alcun punto, come risulta evidente dal fatto che essa sarà costituita "solo da spigoli".
La figura qui sotto mostra il risultato che si ottiene dopo alcuni passaggi. Per rendere più leggibile il disegno le immagini relative a passi successivi sono tracciate su scale diverse.
