Cambiamento di variabile
Riprendendo in esame il teorema sulla continuità della funzione composta di due funzioni continue f e g, possiamo subito concludere con la seguente proposizione:
Se 
e g è una funzione
continua in l, allora 
.
Questo fatto si può anche leggere nel seguente modo: nel calcolare il limite della funzione g(f(x)), posso porre t=f(x), trovare qual è il valore a cui tende la "nuova variabile" t e calcolare poi il limite della funzione g(t), quando t tende a questo valore. In sostanza posso operare un cambiamento di variabile. É una cosa simile a quella che si fa quando si risolve una disequazione biquadratica: ax4 + bx2 + c = 0, quando si pone x2 = t.
Il problema che ci poniamo è il seguente: la tecnica indicata è applicabile anche in altri casi, oltre a quello in cui le funzioni sono continue e il punto sta nel dominio della funzione composta?
Per chiarire la cosa consideriamo un esempio. Si ha:
-
;
-
.
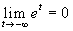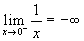Allora: se voglio calcolare 
, posso "porre" 
, osservare che t tende a -∞ e calcolare
? Ossia è vero o no che 
?.
La risposta è affermativa in questo caso e nella maggior parte dei casi che capita di incontrare nelle applicazioni. Purtroppo però esistono situazioni patologiche in cui non si può procedere in questo modo, e per questo bisogna prestare la massima attenzione.
Consideriamo la funzione 
. Avendosi 
e 
, ponendo 
, si otterrebbe 
. Il grafico qui sotto, necessariamente molto
sommario in un intorno di zero, prova invece che tale limite non
esiste.
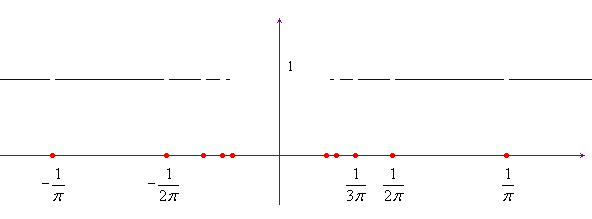
Per completezza proponiamo un teorema che fornisce una condizione sufficiente per l'esistenza del limite nel caso di composizione di funzioni:
Se f e g sono due funzioni tali che si
possa considerare la composta 
e se 
, con la
condizione che f(x)≠l, almeno per x≠c
allora 
. La tesi
è valida anche se l e/o m sono
infiniti. Se poi g è continua in l
oppure non è definita in l, la condizione
f(x)≠l è superflua.
La dimostrazione di questo teorema è simile a quella sulla continuità della funzione composta: la condizione f(x)≠l è quella che consente di concludere. Si controlli come, nell'esempio qui sopra, la non validità di questa condizione è proprio ciò che impedisce l'applicabilità del teorema.