Alcuni limiti fondamentali
Il calcolo dei limiti è un problema molto complesso (tranne ovviamente nel caso delle funzioni elementari in punti del loro dominio). Alcuni limiti di grande importanza nelle applicazioni richiedono un apposito teorema per la loro determinazione: si tratta dei cosiddetti limiti fondamentali, di cui qui proporremo i più importanti. Per la dimostrazione cliccare sul limite prescelto.
-
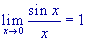(angoli misurati in radianti!).
-
.
-
.
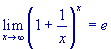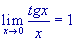Basta solo osservare che tgx=sinx/cosx e ricordare la continuità del coseno.
-
.
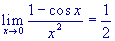Si ha:
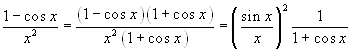. Da qui
la conclusione.
-
.
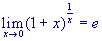Basta operare un cambiamento di variabile 1/x = t, con t che tende all'infinito.
-
.
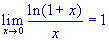Si ha:
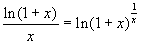da cui
si conclude subito ricordando il limite numero 5.
-
.
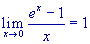Posto
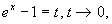ed
x = ln(1+t); si ottiene
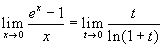, da cui la
conclusione, ricordando il limite 6.
-
.
-
.
-
.
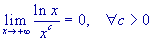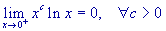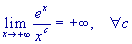Gli ultimi tre limiti possono essere calcolati utilizzando alcune proprietà fondamentali delle funzioni esponenziali e logaritmo, ma il loro calcolo è quasi immediato se si ricorre alla regola di l'Hôpital, che conviene utilizzare.