Funzione inversa
Come è noto una funzione è invertibile se e solo se è biunivoca.
In questo caso si chiama inversa la funzione che ad ogni y del codominio fa corrispondere l'unico x del dominio da cui y proviene. Si può immaginare che con la funzione inversa ciascun bersaglio rispedisce al mittente l'unica freccia da cui è stato colpito. É chiaro che un processo del genere può avere luogo solo con funzioni biunivoche: se la funzione non fosse suriettiva ci sarebbe qualche bersaglio che non è stato colpito da alcuna freccia e quindi non può rispedire alcunché al mittente; se la funzione non fosse iniettiva ci sarebbe qualche bersaglio colpito da più di una freccia e questo tipo di bersagli non saprebbe decidere a quale mittente rispedire le varie frecce da cui è stato colpito.
In sostanza dal punto di vista del grafico si tratta di "invertire" il senso delle frecce.
Per le funzioni reali di variabile reale il grafico dell'inversa di una funzione si ottiene immediatamente scambiando l'asse delle ascisse con quello delle ordinate, cioè facendo il simmetrico del grafico dato rispetto alla bisettrice del primo e terzo quadrante.
Per quanto riguarda le funzioni reali di variabile reale è immediato osservare che se una funzione è strettamente crescente nel suo dominio essa è sicuramente invertibile, ma esistono anche funzioni non crescenti e invertibili: un esempio è fornito dalla funzione \[f(x)=\left\{\begin{array}{rl}x&x\in\mathbb{Q}\\x&x\notin\mathbb{Q}\end{array}\right.\;,\] che non è crescente in nessun intervallo di R, eppure è invertibile in quanto biunivoca: addirittura si tratta di un esempio in cui l'inversa coincide con la funzione stessa.
Il grafico di una funzione e della sua inversa, in uno stesso sistema di assi cartesiani.
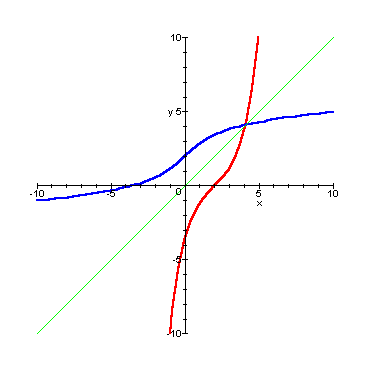
Considerate le proprietà di una funzione e della sua inversa è assolutamente indifferente interpretare l'uno dei due grafici come quello della funzione "diretta" e l'altro come quello della funzione inversa: in ogni caso ciascuno dei due è l'inverso dell'altro.
La retta con colore verde è la bisettrice del primo e terzo quadrante e i punti su di essa rimangono inalterati nel passaggio da una funzione alla sua inversa.
Un'interessante uso delle funzioni inverse si ha nel problema della crittografia.