Cerchi ortogonali
Definizioni e proprietà caratteristiche
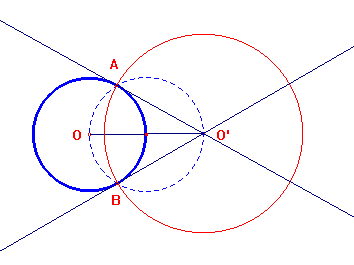
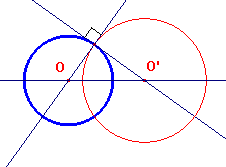
Due cerchi secanti, in un piano π, si dicono ortogonali se le loro tangenti nei punti di intersezione sono perpendicolari. É chiaro che due cerchi sono ortogonali se e solo se le tangenti ad uno nei punti di intersezione passano per il centro dell'altro. Questo equivale a dire che il triangolo OAO' è retto, ovvero che OA2+O'A2=O'O2, relazione che implica che la potenza del centro di un cerchio rispetto all'altro è uguale al quadrato del suo raggio: pO'(O)=r2 e pO(O')=r' 2.
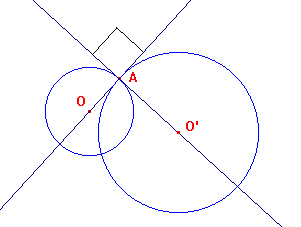
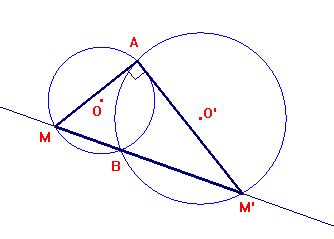
Come conseguenza di una proprietà delle similitudini tra cerchi (che comporta la similitudine tra i triangoli AOO' e AMM'), si deduce anche che due cerchi sono ortogonali se e solo se una secante passante per uno dei due punti comuni è vista dall'altro sotto un angolo retto.
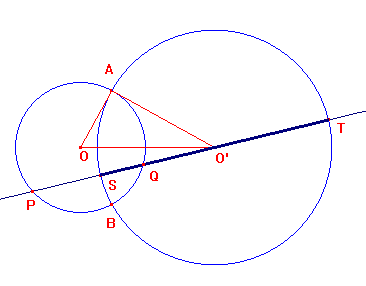
Come ulteriore proprietà caratteristica dei cerchi ortogonali proviamo che due cerchi sono ortogonali se e solo se il diametro di uno dei due cerchi è diviso armonicamente dall'altro. Essendo infatti pO'(O)=O'S2=O'T2 (vedi sopra), si deduce che O'S2=O'Q·O'P che, per una proprietà caratteristica della divisione armonica, implica appunto che P e Q dividono armonicamente il segmento ST.
Cerchi ortogonali ad un cerchio dato
Dato un cerchio O e un punto O', il cerchio O', ortogonale a quello dato, lo interseca nei punti A e B comuni al cerchio O e al cerchio di diametro O'O, ovvero nei punti di tangenza delle tangenti condotte dal punto O' al cerchio O.
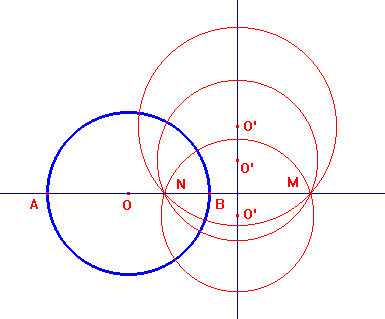
Se è dato il cerchio O e un punto M, considerata la retta OM e il diametro AB appartenente a questa retta, un cerchio O', ortogonale al cerchio O e passante per M, deve passare anche per il punto N tale che M ed N dividano armonicamente il diametro AB. Il luogo dei centri O' di questi cerchi è dunque l'asse di MN, ovvero l'asse radicale del cerchio dato e del cerchio-punto M.
Cerchi ortogonali a due cerchi dati
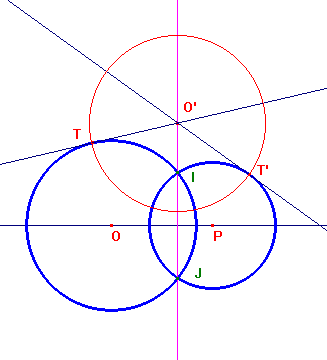
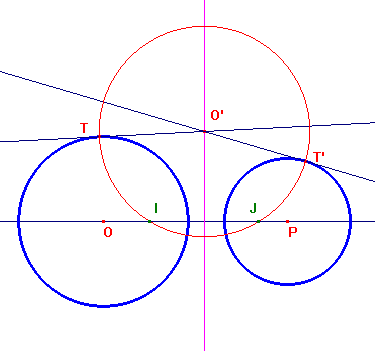
Perché un cerchio O' sia ortogonale a due cerchi O e P, occorre e basta che dal suo centro O' si possano condurre due tangenti OT e OT' tali che i segmenti di tangenza siano uguali. Ciò implica che O' deve stare sull'asse radicale delle due circonferenze, nella parte esterna alle due circonferenze se esse sono secanti. L'insieme di tutti questi cerchi è un fascio di cerchi ortogonale al fascio individuato dai due cerchi dati. Se i due cerchi dati sono secanti, questo fascio ortogonale ha i punti I e J come punti limite, se i due cerchi sono esterni questo fascio ha i punti I e J (punti limite del fascio individuato dai cerchi O e P) come punti base, se i due cerchi dati sono tangenti, questo fascio ortogonale è ancora un fascio tangente nello stesso punto. Si veda un'animazione con CabriJava.
Pseudo-ortogonalità
Dato un cerchio O di raggio r, un cerchio O', di raggio r' taglia diametralmente O se la corda AB che ha come estremi i punti di intersezione dei due cerchi è diametro del cerchio O.Essendo O'O2=r' 2-r2, se ne deduce che pO'(O)=-r2. Per questo motivo il cerchio O' è detto pseudo-ortogonale al cerchio O.
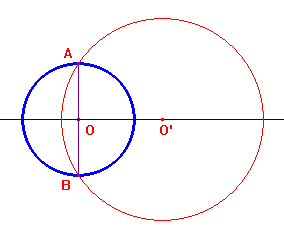
Dati un cerchio O ed un punto O' esiste un unico cerchio O' pseudo-ortogonale ad O: è quello che passa per i punti A e B di intersezione tra il cerchio O e la retta perpendicolare ad O'O. La relazione di pseudortogonalità non è simmetrica: se O' è pseudo-ortogonale ad O, O non è pseudo-ortogonale ad O'.
Osservazione importante
Se è dato un punto fisso O ed un reale k, un cerchio O' tale che la potenza di O rispetto al cerchio O' sia uguale a k gode della seguente proprietà, a seconda che k sia positivo, negativo o nullo:
Se k>0, è ortogonale al cerchio di centro O e raggio k
Se k<0 è pseudo-ortogonale al cerchio di centro O e raggio -k
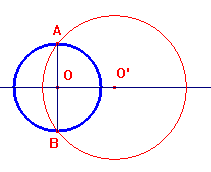
Se k=0 è ortogonale (o, il che è lo stesso, pseudo-ortogonale) al cerchio punto O, cioè passa per il punto O.