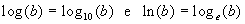Logaritmi: sfatiamo un mito
E', crediamo, un'esperienza abbastanza comune il fatto che, al primo accenno dei logaritmi (secondo-terzo anno di scuola superiore), in genere gli studenti storcono il naso: è come se un'informazione sulla difficoltà di questo capitolo della matematica permeasse i muri delle aule scolastiche e si tramandasse da una generazione di allievi alla successiva.
Vorremmo cercare, con questa paginetta dall'impostazione assolutamente informale, di ribaltare la situazione, facendo vedere come l'introduzione dei logaritmi non sia assolutamente una cosa complicata, o meglio, non più complicata dello studio dei radicali, che tanta parte (sicuramente troppa!) occupano nel curricolo degli studenti.
Segnaliamo che non intendiamo qui proporre una trattazione sistematica dei logaritmi, ma solo un metodo per rendere più facile questo nuovo concetto, valutando le analogie con quello, familiare(!), di radice.
Premessa (un po' lunga!) sulle notazioni
Per comprendere a fondo il problema di cui vogliamo occuparci, è opportuno fare una riflessione sulle notazioni utilizzate per scrivere i radicali. In questo sito abbiamo proposto anche una discussione dettagliata sul problema della definizione della funzione radice quadrata. Si possono leggere anche alcune considerazioni sulle proprietà dei radicali considerati come sottoinsieme dei reali.
Dato il numero reale a e il naturale n≥2,
il simbolo comunemente usato per rappresentare l'unica sua
radice n-esima positiva, se a≥0 e
n pari, oppure l'unica sua radice n-esima,
se a è un reale qualunque e n dispari,
è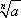 
. Questo simbolo
non può essere utilizzato nella scrittura dei programmi
per pc, per il fatto che è scritto su diversi livelli
(l'indice n in alto, mentre il radicando a
in basso) e per la presenza della barra orizzontale che serve a
racchiudere tutto il radicando, come una coppia di parentesi
(questa barra orizzontale era usata normalmente, nella
matematica antica, al posto delle attuali parentesi: si
scriveva, per esempio, 
,
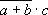al posto di (a+b)·c, come noi oggi
scriviamo). Per le radici quadrate si potrebbe, per evitare
questa difficoltà, abolire l'indice (come di solito
si fa) e sostituire la barra orizzontale con una coppia di
parentesi, ottenendo una scrittura del tipo √(a).
Questa scelta risolverebbe il problema della radice quadrata
(che è la più usata e comune), ma introdurrebbe un
nuovo simbolo che non appartiene al sistema di caratteri di base
riconosciuti da tutti i pc (quelli del codice ASCII base).
Alcuni software in commercio (es.Derive) tollerano questa
simbologia, ma la scelta comune è di natura completamente
diversa: la radice quadrata di a è, quasi
universalmente, indicata con sqrt(a). Si usa porre,
cioè:
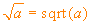
Naturalmente sqrt sta per "square root". Un'eccezione a questa scelta è quella di Excel (e l'analogo software di OpenOffice), dove viene usato radq(a) in sostituzione di sqrt(a). Quello che ci preme qui segnalare è che questa notazione è conforme alla regola di base sulle funzioni: nella scrittura f(x) adottata per una funzione si dovrebbero evidenziare tre parti, e precisamente
- un simbolo per la funzione: f
- un simbolo per la variabile indipendente: x
- una coppia di parentesi che racchiudono la variabile: (·).
Nella scrittura sqrt(a), queste tre parti sono
evidenti, come anche in √(a). Nel caso di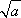 
, invece, mancano le parentesi
tonde. In una scrittura per esseri intelligenti è ovvio
che questo non costituisce un problema; nel caso degli automi
esecutori non pensanti (come è nella sostanza un
computer), invece, una convenzione di questo tipo potrebbe
provocare difficoltà insormontabili. I computer hanno
bisogno di un rigore formale assoluto. Esistono, per la
verità, eccezioni, come per esempio i software di calcolo
simbolico (es. Derive), ma sono circoscritte e limitate a casi
particolari. Il problema delle notazioni, in matematica, non
è comunque mai un problema semplice; per quel che
riguarda le funzioni puoi leggere alcune considerazioni nella pagina
sulle notazioni.
Per lo scopo che ci prefiggiamo di raggiungere con queste
osservazioni, comunque, ci serve un simbolo che tratti anche il
caso delle radici n-esime, per tutti i valori di
n≥2. Una delle possibili scelte (fatta anche
nelle calcolatrici tascabili) è quella di ricondurre una
radice n-esima ad una potenza, con varie notazioni. Per
esempio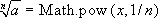 
è la
scelta di Javascript. In questo caso la difficoltà sta
nel fatto che i due argomenti della funzione (quelli tra
parentesi tonde) hanno significati completamente diversi.
Senza ulteriormente insistere su questo argomento (potremmo
parlare per ore senza giungere ad un accordo soddisfacente!),
proponiamo di adottare, almeno fino alla fine di questa pagina,
la seguente convenzione: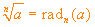 
, scrittura che leggeremo radice, di
indice n, di a.
Introduzione parallela delle radici e dei logaritmi
Utilizzando la tabella qui sotto proponiamo ora una introduzione dei logaritmi che ripercorra pari pari l'analoga introduzione delle radici.
Radici |
Logaritmi |
|
Consideriamo l'equazione x2 = b.
Se b è un numero reale positivo, essa
ha due soluzioni opposte che, secondo le convenzioni
appena adottate, indicheremo con
x1,2 = ±rad2(b) |
Consideriamo l'equazione 2x = b. Se b è un
numero reale strettamente positivo, essa ha una sola
soluzione, per la quale adotteremo, in analogia al caso
delle radici, la notazione
x = log2(b) |
| In sostanza questo equivale a dare la seguente definizione: dato un numero reale positivo b, si chiama radice di indice 2 di b l'unico numero positivo che, utilizzato come base per una potenza di esponente 2, dà come risultato b. | In sostanza questo equivale a dare la seguente definizione: dato un numero reale strettamente positivo b, si chiama logaritmo di base 2 di b l'unico numero che, utilizzato come esponente per una potenza di base 2, dà come risultato b. |
| Come si vede si tratta sostanzialmente dello stesso problema, risolto in maniera analoga, con la facilitazione, nel caso dei logaritmi, legata al fatto che l'equazione che stiamo considerando ha una sola soluzione, invece di due. La differenza tra i due casi consiste semplicemente nello scambio della parola base con la parola esponente. | |
|
Consideriamo ora l'equazione x3 = b.
Se b è un numero reale qualunque, essa
ha una sola soluzione che, secondo le convenzioni
appena adottate indicheremo con
x = rad3(b) |
Consideriamo ora l'equazione 3x = b.
Se b è un numero reale strettamente
positivo, essa ha una sola soluzione, per la quale
adotteremo, in analogia al caso delle radici, la
notazione
x = log3(b) |
| In sostanza questo equivale a dare la seguente definizione: dato un numero reale b, si chiama radice di indice 3 di b l'unico numero che, utilizzato come base per una potenza di esponente 3, dà come risultato b. | In sostanza questo equivale a dare la seguente definizione: dato un numero reale strettamente positivo b, si chiama logaritmo di base 3 di b l'unico numero che, utilizzato come esponente per una potenza di base 3, dà come risultato b. |
|
Ripetendo quanto già detto sopra possiamo notare
che anche ora l'unica differenza sostanziale tra il
caso delle radici e quello dei logaritmi è nella
sostituzione della parola base con la
parola esponente. Possiamo però
anche osservare che nel caso dei logaritmi il passaggio
dalla base due alla base non ha cambiato quasi nulla,
mentre nel caso delle radici c'è una
modifica di fondo: con esponente 2 si avevano due
soluzioni, con la condizione che b fosse
positivo, con esponente tre si ha sempre una sola
soluzione, qualunque sia il valore di b.
Questo significa che il concetto di logaritmo è, logicamente, molto più semplice che non quello di radice. Passiamo ora al caso di un esponente o di una base generica. Abbiamo, passando dalle radici ai logaritmi, una nuova semplificazione notevole: nel caso delle radici l'indice è, convenzionalmente, sempre un naturale ≥2; nel caso dei logaritmi la base potrà essere un reale strettamente positivo qualunque (quindi anche non intero), con la sola eccezione del valore 1, in quanto 1x fa sempre 1 e quindi non ha senso considerare equazioni del tipo 1x = b. Il Per questo indicheremo con n l'indice generico della radice e invece con a la base generica dei logaritmi. Il caso delle basi negative, per i logaritmi, non ha interesse in quanto le potenze che hanno esponenti non interi richiedono basi positive. |
|
|
Consideriamo l'equazione xn = b. Dobbiamo distinguere due casi.
|
Consideriamo l'equazione ax = b. Se a è un numero reale strettamente positivo e diverso da 1, e b è numero un reale strettamente positivo, essa ha una sola soluzione, che indichiamo con x = loga(b) |
| In sostanza questo equivale a dare la seguente definizione: dato un numero naturale pari n≥2 e un numero reale positivo b, si chiama radice di indice n di b l'unico numero positivo che utilizzato come base per una potenza di esponente n, dà come risultato b; dato invece un numero naturale dispari n≥3 e un numero reale qualunque b, si chiama radice di indice n di b l'unico numero che, utilizzato come base per una potenza di esponente n, dà come risultato b. | In sostanza questo equivale a dare la seguente definizione: dati un numero reale a strettamente positivo e diverso da 1, e un numero reale strettamente positivo b, si chiama logaritmo di base a di b l'unico numero che, utilizzato come esponente per una potenza di base a, dà come risultato b. |
|
Non occorre grande fantasia per concludere che la colonna di destra contiene situazioni molto più facili da trattare che non quella di sinistra! |
|
|
Casi particolari Il caso n=2 è talmente frequente nelle applicazioni, che per esso si usa un simbolo semplificato, abolendo del tutto l'indicazione dell'indice. Si scrive dunque, ritornando alla scrittura tradizionale:
|
Casi particolari Nel caso dei logaritmi ci sono due casi particolarmente importanti nelle applicazioni, quello con a=10 e quello con a=e (ove e è il cosiddetto Numero di Nepero, un irrazionale trascendente che vale, all'incirca, 2.718). Si usano le notazioni:
|
