Il piano di Gauss - Forma trigonometrica
Piano di Gauss
Ancor più che nel caso dei numeri
reali, una opportuna rappresentazione grafica dei complessi
è cruciale per trattare i problemi che li coinvolgono. Il
modo con cui questi numeri sono stati introdotti porta
immediatamente a concludere che la rappresentazione grafica
"naturale" è quella in un piano cartesiano, che
chiameremo piano di Gauss o anche di
Argand-Gauss. L'asse delle ascisse si chiama anche
asse reale mentre quello delle ordinate asse
immaginario.
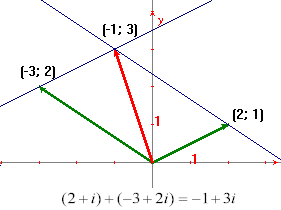
Tenendo conto di come è stata definita la somma, i numeri complessi potranno essere anche pensati come vettori di questo piano (con l'origine in O): la somma si fa esattamente come la somma di vettori, con la regola del parallelogramma.
Forma trigonometrica o polare
Più difficile l'interpretazione grafica del prodotto, per la quale conviene introdurre una diversa scrittura dei numeri complessi. Per questo rappresentiamo il numero complesso z=x+iy nel piano di Gauss e consideriamone il modulo (che non è altro che la distanza del punto (x,y) dall'origine). Consideriamo poi la semiretta orientata uscente dall'origine e passante per z.
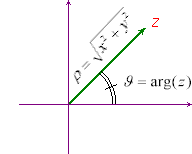Si chiama argomento principale
di z, e si indica con Arg(z),
l'angolo che questa semiretta forma con il semiasse positivo
delle x, orientato in senso antiorario e appartenente a
[0,360[, o [0,2π[ se si usano (come è preferibile) i
radianti. In alcuni testi la convenzione è leggermente
diversa: [0,360[, o [0,2π[ sono sostituiti con ]-180,180], o
]-π,π]. E' chiaro che la rappresentazione di un numero
complesso x+iy mediante una coppia
(modulo,argomento principale) è univoca, con la
sola eccezione del punto 0, per il quale non risulta definito un
argomento principale. In molte questioni è utile
rimuovere le limitazioni poste per l'argomento principale,
ammettendo anche valori dell'angolo superiori a π o
inferiori a -π: in questo caso si parla di solito di
argomento (che si indica con arg(z)) senza
l'aggettivo principale ed è ovvio che la
rappresentazione non è più univoca. Questo
però non porta complicazioni particolari nel trattare i
complessi e anzi facilita molti calcoli.
Dunque un numero complesso può essere rappresentato con la coppia (modulo,argomento), anziché con la coppia (parte reale,parte immaginaria): nel primo caso si avrà la forma trigonometrica, detta a volte anche polare, nel secondo la ormai tradizionale forma algebrica. Per non fare confusione tra le due si usa per la prima la scrittura con le parentesi quadre, per la seconda quella, già considerata e comune per le coppie, con le parentesi tonde: x+iy = (x,y) = [ρ,θ].
Si noti che due numeri
z1=(x1,y1)
= [ρ1,θ1] e
z2=(x2,y2)
=
[ρ2,θ2]
sono uguali se e solo se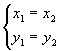 
o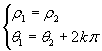 
, a seconda che i numeri siano in forma
algebrica o polare.
Passaggio da una forma all'altra
Il passaggio dalla forma polare a quella algebrica si fa in modo
banale, tenendo conto della definizione delle funzioni seno e
coseno: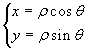 
. Da qui si deduce la seguente
scrittura z = x+iy =
ρ(cosθ+isinθ):
spesso è più propriamente quest'ultima
scrittura che è nota come forma trigonometrica.
Il passaggio inverso è immediato per quanto riguarda la
ricerca del modulo: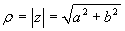 
. Per la ricerca dell'argomento basta
utilizzare le formule inverse delle precedenti: 
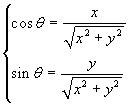. Si
presti attenzione a determinare preventivamente il quadrante in
cui si trova θ, esaminando il segno del suo
coseno e del suo seno, dopodiché mediante una delle due
formule si potrà trovare l'angolo.
Prodotto e quoziente in forma trigonometrica
Dati due complessi z=x+iy=ρ(cosθ+isinθ) e w=s+it=r(cosφ+isinφ), calcoliamone il prodotto e il quoziente, considerando la forma trigonometrica:
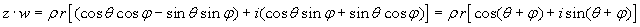
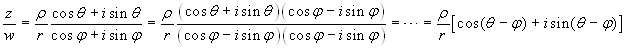
Questo ci autorizza a scrivere le seguenti importanti formule:
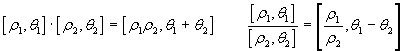
Dalla prima di queste due formule si può ricavare come caso particolarmente importante la seguente conseguenza per la potenza n-esima di un complesso:
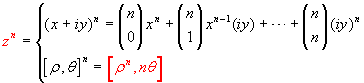
La seconda formula scritta si chiama formula di De Moivre. Si noti come essa sia decisamente più semplice della prima, che coinvolge il binomio di Newton. Essa è inoltre, come vedremo, alla base della formula per il calcolo delle radici di un numero complesso. La dimostrazione utilizza il principio di induzione: essa è ovviamente vera per n=1; supposta vera per n-1 un semplice calcolo mostra che è vera anche per n (basta moltiplicare [ρ,θ] per [ρn-1,(n-1)θ]).
Prodotto e rotazioni
La formula ricavata sopra consente di dare una semplice interpretazione geometrica al prodotto di due numeri complessi: il prodotto tra il numero complesso z=x+iy=ρ(cosθ+isinθ) e il numero complesso w=s+it=r(cosφ+isinφ) può essere interpretato come una dilatazione del vettore che rappresenta z (dilatazione del fattore r=|w|) seguita da una sua rotazione di un angolo φ. Se, in particolare, w ha modulo 1 si tratta di una semplice rotazione. Molto importante il caso che w=i, nel qual caso si tratta di una rotazione di 90°.
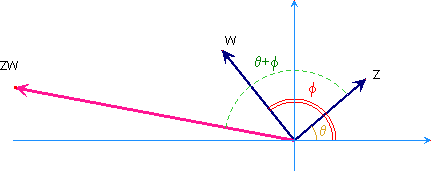
Questa proprietà dei complessi introduce un importante legame tra questi numeri e le trasformazioni geometriche del piano ed ha numerose applicazioni nella fisica e in particolare nell'elettrotecnica (studio di circuiti in corrente alternata).