Prime proprietà
Complessi e ordine
L'insieme dei numeri complessi è dunque un ampliamento dei reali, di cui mantiene alcune caratteristiche molto importanti, quali la struttura algebrica. C'è però una sostanziale differenza, che apparirà naturale quando parleremo del piano di Gauss: in questo insieme non è possibile introdurre un ordine che abbia un qualche interesse.
Ricordiamo che su ogni insieme è possibile introdurre addirittura un buon ordinamento, ovvero un ordinamento simile a quello che c'è sui naturali (ogni insieme non vuoto e inferiormente limitato ha un minimo), ma in generale perché un ordinamento su un insieme con struttura abbia interesse occorre che esso sia compatibile con le operazioni della struttura stessa. Quello che ci interessa è che l'insieme, diciamolo K, sia un corpo (commutativo) ordinato, ovvero che:
-
Siano definite due operazioni (addizione e moltiplicazione)
dotate di:
- proprietà associativa
- esistenza di elemento neutro
- esistenza di reciproco
- proprietà commutativa
- proprietà distributiva della moltiplicazione rispetto all'addizione
- Sull'insieme sia definito un ordine totale (due elementi sono sempre confrontabili)
-
Se definiamo
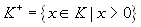 , valgono le seguenti
proprietà:
, valgono le seguenti
proprietà:
-
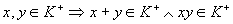 ;
;
-
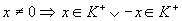 ;
;
-
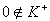 ;
;
-
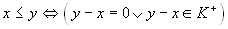 .
.
-
E' facile provare che tutte queste proprietà non possono essere verificate contemporaneamente sul corpo dei complessi.
Dunque non esiste possibilità di introdurre nell'insieme dei complessi una qualche forma di ordine: dati due complessi qualunque potremo solo dire se essi sono uguali o diversi, mentre non avremo alcuna possibilità di decidere quale dei due è il più grande né, tantomeno, di decidere se un complesso è positivo o negativo.
Il modulo di un numero complesso
Dato un numero complesso z = a+ib, chiameremo
suo modulo il numero reale positivo 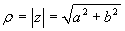 . Per il modulo
valgono proprietà analoghe a quelle già viste per
i numeri reali. In particolare segnaliamo che:
. Per il modulo
valgono proprietà analoghe a quelle già viste per
i numeri reali. In particolare segnaliamo che:
- |z+w| ≤ |z| + |w|
- |zw| = |z| |w|
La dimostrazione è una pura questione di calcoli.
E' importante notare alcune differenze operative tra il modulo nei reali e quello nei complessi. Esaminiamo alcuni esempi.
![]() |z|2 ≠
z2. Il primo infatti è un numero
reale positivo, il secondo no: |z|2 =
a2+b2, mentre
z2 =
a2-b2+2iab.
|z|2 ≠
z2. Il primo infatti è un numero
reale positivo, il secondo no: |z|2 =
a2+b2, mentre
z2 =
a2-b2+2iab.
![]() |z|2 =
|z2|. Il primo membro vale
a2+b2, per il secondo si
ha
|z|2 =
|z2|. Il primo membro vale
a2+b2, per il secondo si
ha 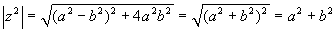 , da cui l'uguaglianza.
, da cui l'uguaglianza.
![]()
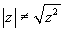 . Per convincersene si può
provare prendendo z=i: al primo membro si ottiene 1, al
secondo membro ±i. Questa osservazione è
particolarmente importante, in quanto nei reali il modulo di un
numero x può anche essere definito mediante
. Per convincersene si può
provare prendendo z=i: al primo membro si ottiene 1, al
secondo membro ±i. Questa osservazione è
particolarmente importante, in quanto nei reali il modulo di un
numero x può anche essere definito mediante 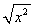 . Si
noti anche che abbiamo scritto che il secondo membro vale
±i. La cosa può apparire strana, in
quanto nei reali con il simbolo
. Si
noti anche che abbiamo scritto che il secondo membro vale
±i. La cosa può apparire strana, in
quanto nei reali con il simbolo 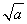 si indica un solo numero,
se a>0, non due. La convenzione è
diversa sui complessi, come vedremo.
si indica un solo numero,
se a>0, non due. La convenzione è
diversa sui complessi, come vedremo.
Il coniugato di un numero complesso
Dato un numero complesso z = a+ib,
chiameremo suo coniugato il numero 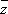 = a-ib. L'operazione
che fa passare da un complesso al suo coniugato gode di alcune
interessanti proprietà che si possono verificare con
semplici calcoli e sono lasciate per esercizio.
= a-ib. L'operazione
che fa passare da un complesso al suo coniugato gode di alcune
interessanti proprietà che si possono verificare con
semplici calcoli e sono lasciate per esercizio.
-
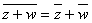 ;
;
-
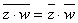 ;
;
-
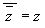 ;
;
-
z
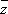 =
|z|2;
=
|z|2;
-
z =
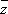 se e
solo se z è reale;
se e
solo se z è reale;
-
z +
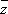 è
sempre reale.
è
sempre reale.