L'algebra delle derivate
In questa pagina ci occupiamo del seguente problema: se due funzioni sono derivabili, che ne è della loro somma, prodotto o quoziente? Visto che la derivata è sostanzialmente un limite (finito per giunta!), e che i limiti si comportano in maniera carina nei confronti delle operazioni elementari, c'è da aspettarsi che altrettanto succeda per le derivate: in effetti è proprio così, come dice il seguente
Teorema: Se f e g sono due funzioni definite in un intervallo comune e derivabili in un punto c, allora:
- f+g è derivabile in c e si ha (f+g)' = f' + g'; dim
- f·g è derivabile in c e si ha (f·g)' = f'·g + f·g' (regola della catena o anche regola di Leibniz); dim
-
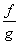 è derivabile in
c (ovviamente purché il denominatore non
si annulli) e si ha:
è derivabile in
c (ovviamente purché il denominatore non
si annulli) e si ha: 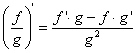 . dim
. dim
Si noti che questo teorema esprime solo una condizione sufficiente per la derivabilità di una somma, prodotto, quoziente. É facile portare esempi che comprovano la non necessità della condizione espressa.
Esempio 1. Le funzioni f(x) = |x| e g(x) = -|x| non sono derivabili nell'origine, ma la loro somma ovviamente si, visto che è la funzione identicamente nulla, ma forse questo esempio è troppo cretino.
Esempio 2. Si considerino le due funzioni 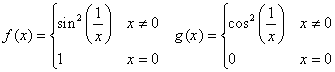 . Esse non sono nemmeno continue nell'origine,
per cui non possono essere derivabili. La loro somma è la
funzione costantemente uguale ad 1, e quindi è certamente
derivabile.
. Esse non sono nemmeno continue nell'origine,
per cui non possono essere derivabili. La loro somma è la
funzione costantemente uguale ad 1, e quindi è certamente
derivabile.
Esempio 3. Si considerino le funzioni f(x)
= x e g(x) = |x|. La prima è derivabile,
mentre la seconda no (nell'origine). Il loro prodotto
è invece derivabile anche nell'origine, come prova il
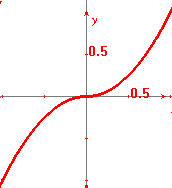
calcolo seguente: ![]() . Il grafico qui sotto
rende evidente che la curva è costituita da due rami di
parabola (y=x2 e y=-x2)
che nell'origine si saldano senza spigoli. Un esempio ancora
più semplice è dato dal prodotto della funzione
modulo (non derivabile nell'origine) per se stessa, che
coincide con la funzione f(x)=x2 (ovviamente
sempre derivabile).
. Il grafico qui sotto
rende evidente che la curva è costituita da due rami di
parabola (y=x2 e y=-x2)
che nell'origine si saldano senza spigoli. Un esempio ancora
più semplice è dato dal prodotto della funzione
modulo (non derivabile nell'origine) per se stessa, che
coincide con la funzione f(x)=x2 (ovviamente
sempre derivabile).
La linearità dell'operatore derivata
Una immediata conseguenza del teorema è che se k è una costante (kf)' = kf'. Consideriamo allora l'insieme di tutte le funzioni definite su un comune intervallo e derivabili in uno stesso punto c. Allora l'operazione di derivazione gode delle due proprietà seguenti:
- (kf)' = kf' ;
- (f+g)' = f' + g'.
In sostanza l'operazione di derivazione si comporta in maniera decente rispetto alle operazioni di somma e prodotto per un numero. Si esprime questo fatto dicendo che l'operazione di derivazione gode della proprietà di linearità. Inoltre il fatto che la somma di due funzioni derivabili e il prodotto di una funzione derivabile per un numero sia ancora derivabile implica che l'insieme delle funzioni in oggetto è uno spazio vettoriale.