La derivata di una funzione composta
La regola che permette di calcolare la derivata della composta di due funzioni è della massima importanza, in quanto la maggior parte delle funzioni di uso comune è costruita componendo opportunamente le funzioni elementari.
Prima di introdurre la regola è però opportuna una precisazione sulle notazioni. Come si può vedere in dettaglio in questa pagina, la scrittura usata per le funzioni è spesso difficile da leggere. Il problema di individuare chiaramente quali siano le funzioni (elementari) che compongono una data funzione, diventa cruciale quando si vuole applicare la regola di derivazione delle funzioni composte. Chiariamo il fatto con un esempio.
Esempio. Si consideri la funzione 
. Essa può essere pensata come la composta
delle funzioni 
. É utile farsi uno
schema (anche se non sempre per iscritto!), come quello qui
sotto:
.
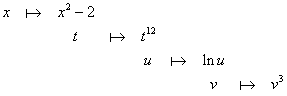Da qui appare evidente come venga costruita la funzione composta attraverso i suoi passi elementari: la prima funzione (diciamola g) produce come risultato x2-2; questo diventa il punto di partenza per la seconda funzione (diciamola h), la cui variabile indichiamo con t e che produce come risultato t12; questo a sua volta diventa la variabile (u) della terza funzione (diciamola l), che produce come risultato lnu; infine si applica l'ultima funzione (diciamola m, agente sulla variabile di nome v), che dà come risultato v3. Si può scrivere f(x)=m(l(h(g(x)))).
Consideriamo allora due funzioni f e g, tali che sia possibile costruire la composta h=f°g, e consideriamo un punto c del dominio della composta. Vale il seguente
Teorema. Date due funzioni f e g, tali che sia possibile costruire la composta h=f°g, e considerato un punto c del dominio della composta, indichiamo con d il valore g(c). Allora: se g è derivabile in c e f è derivabile in d=g(c), la funzione composta è derivabile in c e si ha:
ovvero 
.
Puoi vedere una dimostrazione per via grafica di questo teorema.
Ci si può rendere comunque conto, in maniera grossolana, del significato di questo teorema con il seguente ragionamento. Con riferimento al precedente enunciato, supponiamo, per fissare le idee, che (Df)(d)=3 e (Dg)(c)=4, e poniamo t=g(x). Allora un piccolo incremento Δx di c provoca un incremento di t circa 4 volte più grande: Δt=4Δx. D'altro canto il fatto che la derivata di f (in d!) sia 3, significa che un piccolo incremento Δt di d provoca un incremento di y circa 3 volte più grande: Δy=3Δt. E' allora chiaro che il rapporto tra Δx e Δy sarà circa di 1 a 12.
Esempio 1 Calcolare la derivata di h(x)=sinx2. In questo caso si ha g(x)=x2, e f(t)=sint. Tenendo conto che g'(x)=2x mentre f'(t)=cost, si ottiene h'(x)=cosx2·2x.
Esempio 2. Calcolare la derivata di 
. Si ha 
, da cui 
.
Esempio 3. Calcolare la derivata di h(x)=(x-2)27. Si ha g(x)=x-2, f(t)=t27, g'(x)=1, f'(t)=27t26, da cui h'(x)=27(x-2)26.