Funzioni esponenziali e logaritmiche
Premessa
Anche per queste disequazioni, come per quelle irrazionali, non esistono regole generali per la risoluzione e anche disequazioni molto semplici sono generalmente risolubili solo con metodi numerici, come si può vedere dai seguenti esempi.
Esempio 1. Risolvere la disequazione
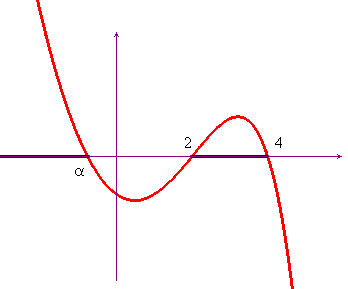
x2 - 2x > 0. Il grafico qui
sotto mostra che la disequazione è verificata per
x<α ![]() 2<x<4. Mentre i valori x=2 e
x=4 si possono trovare in via elementare (il primo
è banale, il secondo è la famosa coppia di reali
per cui xy=yx), il valore di
α si può solo trovare con metodi numerici (lo
stesso Cabri con cui è fatto il grafico trova x
2<x<4. Mentre i valori x=2 e
x=4 si possono trovare in via elementare (il primo
è banale, il secondo è la famosa coppia di reali
per cui xy=yx), il valore di
α si può solo trovare con metodi numerici (lo
stesso Cabri con cui è fatto il grafico trova x ![]() -0.77).
-0.77).
Disequazioni elementari
Considerati un reale a positivo e diverso da uno e un reale b qualunque, si dicono elementari le disequazioni del tipo:
- ax > b
- ax < b
- ax ≥ b
- ax ≤ b
- logax > b
- logax < b
- logax ≥ b
- logax ≤ b
Esse sono di fondamentale importanza, perché le tecniche applicabili alle disequazioni esponenziali e logaritmiche si basano sulla risoluzione di questo tipo di disequazioni.
Per risolvere questo tipo di disequazioni è conveniente ricordare i grafici delle funzioni esponenziali e logaritmiche e le loro proprietà essenziali. Li riportiamo qui sotto per comodità.
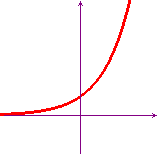
f(x) = ax, con a>1
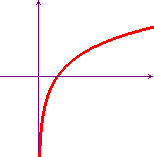
f(x) = logax, con a>1
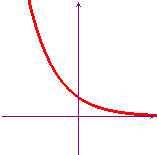
f(x) = ax, con a<1
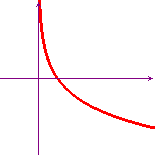
f(x) = logax, con a<1
In matematica si usa quasi sempre come base dei logaritmi e delle funzioni esponenziali il numero di Nepero "e", che è maggiore di 1, per cui i primi due grafici sono di gran lunga i più importanti e ad essi faremo usualmente riferimento. Per la definizione di logaritmo il secondo grafico non è altro che il simmetrico del primo rispetto alla bisettrice y=x (altrettanto dicasi del quarto rispetto al terzo). Per risolvere le disequazioni è molto importante saper leggere con disinvoltura questi grafici.
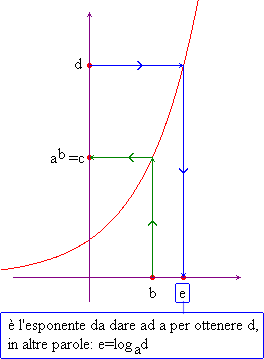
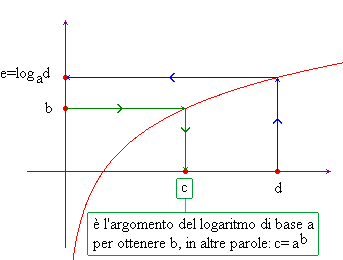
Nel primo grafico (funzione esponenziale di base a maggiore di 1), a partire da un punto b sull'asse delle ascisse e seguendo il percorso verde si trova il risultato c della potenza ab. A partire invece da un punto d sull'asse delle ordinate e seguendo il percorso blu si trova sull'asse delle ascisse l'esponente e che si deve dare ad a per avere d.
Nel caso per esempio di a=2, a partire da b=3
si trova c=8, a partire da d=32 si trova
e=5.
Il secondo grafico fa le stesse cose, ma con punti di partenza invertiti: a partire da un punto d sull'asse delle ascisse si trova sull'asse delle ordinate il suo logaritmo in base a. A partire invece da un punto b sull'asse delle ordinate e seguendo il percorso verde si trova sull'asse delle ascisse l'argomento del logaritmo di base a per avere b.
Nel caso per esempio di a=10, a partire da d=1000 si trova e=3, a partire da b=2 si trova c=100.
Tenendo conto di questi grafici e del loro significato la risoluzione delle disequazioni elementari è immediata, come si può vedere dai due esempi che seguono.
Esempio 1. Risolvere la disequazione
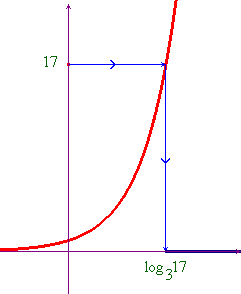
3x > 17. Tracciato il grafico della
funzione f(x)=3x, e fissato il valore 17
sull'asse delle ordinate, si tratta di trovare i valori di
x che dati come esponente a 3 producono una potenza
maggiore di 17. Il grafico qui sotto rende immediatamente
evidente che la soluzione è: x >
log317.
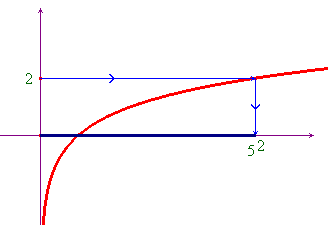
Esempio 2. Risolvere la disequazione log5x ≤ 2. Tracciato il grafico della funzione f(x)=log5x, e fissato il valore 2 sull'asse delle ordinate, si tratta di trovare i valori di x (argomento del logaritmo) che hanno un logaritmo non superiore a 2. Il grafico qui sotto rende immediatamente evidente che la soluzione è: 0 < x ≤ 52.
La tecnica proposta in questi due esempi può essere applicata in tutti gli altri casi e, a nostro avviso, è da preferire ad altre tecniche analitiche, soprattutto per le disequazioni con il logaritmo dove è facile dimenticare le condizioni per l'esistenza. Si tratta solo di acquisire un po' di pratica nella lettura dei grafici, pratica che comunque è utile in moltissime altre circostanze.
Le altre disequazioni
Come già accennato all'inizio non esistono tecniche specifiche per risolvere queste disequazioni e solo in alcuni casi si riesce a ricondursi, usando le proprietà delle potenze e dei logaritmi, oppure opportune sostituzioni, alla risoluzione di una o più disequazioni elementari. Gli esempi che proporremo daranno utili indicazioni sui metodi da seguire.
Esempio 1. Risolvere la disequazione:
2x+1 > 5 - 4x-1. La
disequazione si può trasformare come segue: ![]() ,
, ![]() ,
, ![]() .
A questo punto, posto 2x=t, si ottiene, dopo
opportuna semplificazione, t2 + 8t - 20 >
0. Questa disequazione è verificata per
t<-10
.
A questo punto, posto 2x=t, si ottiene, dopo
opportuna semplificazione, t2 + 8t - 20 >
0. Questa disequazione è verificata per
t<-10 ![]() t>2. Si deve dunque risolvere
t>2. Si deve dunque risolvere ![]() .
La prima disequazione non ha alcuna soluzione, la seconda
è verificata per x>1, che è anche la
soluzione della disequazione data.
.
La prima disequazione non ha alcuna soluzione, la seconda
è verificata per x>1, che è anche la
soluzione della disequazione data.
Nello stesso modo si possono risolvere tutte le disequazioni in
cui compare solo ax o
logax, purché la sostituzione
t=ax o t=logax porti ad
una disequazione che si sappia risolvere. In termini precisi si
tratta di disequazioni del tipo f(ax)>0
o
f(logax)>0, dove
f(t)>0 è una disequazione risolubile.
É la stessa tecnica che si applica, per esempio, per le
biquadratiche, dove si pone x2=t e ci si
riconduce ad una equazione, o disequazione, di secondo grado.
Altri esempi simili, che si può provare a risolvere,
sono: ![]() .
.
Esempio 2. Risolvere la disequazione
log5(x-3) - log5(5-x) > 0. Si
trova, innanzitutto, il dominio:
![]() . Dopodiché si
può scrivere:
. Dopodiché si
può scrivere: ![]() . Si noti che
abbiamo eliminato il denominatore 5-x perché
sicuramente positivo in base al dominio. Tenendo conto del
dominio si conclude che l'insieme di soluzioni è
4<x<5. Si noti che siamo passati alla forma
. Si noti che
abbiamo eliminato il denominatore 5-x perché
sicuramente positivo in base al dominio. Tenendo conto del
dominio si conclude che l'insieme di soluzioni è
4<x<5. Si noti che siamo passati alla forma ![]() solo dopo aver trovato il
dominio: anche se in questo caso il dominio in
quest'ultima forma è lo stesso di prima, in generale
non è vero che
solo dopo aver trovato il
dominio: anche se in questo caso il dominio in
quest'ultima forma è lo stesso di prima, in generale
non è vero che
log(x)-log(y)=log(x/y); basta pensare a
log(-2)-log(-3) che non ha senso, e quindi non
può essere uguale a
log(-2/-3)=log(2/3) che invece ha senso.
Esempio 3. Risolvere la disequazione ![]() . Si possono considerare i passaggi seguenti:
. Si possono considerare i passaggi seguenti: ![]() . Questa è una disequazione elementare, la
cui soluzione è x>0 (si tenga conto che 3/5
è minore di 1!).
. Questa è una disequazione elementare, la
cui soluzione è x>0 (si tenga conto che 3/5
è minore di 1!).
Esempio 4. Risolvere la disequazione ![]() . Si deve trovare innanzitutto il dominio:
. Si deve trovare innanzitutto il dominio: 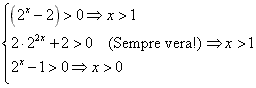 . Dopodiché si pone
2x=t e si usano le proprietà dei
logaritmi. Si ottiene facilmente:
. Dopodiché si pone
2x=t e si usano le proprietà dei
logaritmi. Si ottiene facilmente: ![]() ,
che ha come soluzioni -3<t<0. Se ne deduce subito
che la disequazione data non ha soluzioni
(2x non può essere negativo!).
,
che ha come soluzioni -3<t<0. Se ne deduce subito
che la disequazione data non ha soluzioni
(2x non può essere negativo!).
Esempio 5. Risolvere la disequazione ![]() . Occorre innanzitutto trovare il dominio. Si
può scrivere:
. Occorre innanzitutto trovare il dominio. Si
può scrivere: 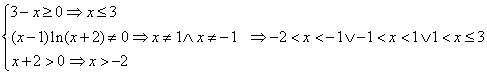 . Dopodiché
si trova il segno di ognuno dei tre fattori che compaiono a
primo membro e si costruisce il solito grafico del tipo +/-.
Riportiamo solo il grafico finale.
. Dopodiché
si trova il segno di ognuno dei tre fattori che compaiono a
primo membro e si costruisce il solito grafico del tipo +/-.
Riportiamo solo il grafico finale.
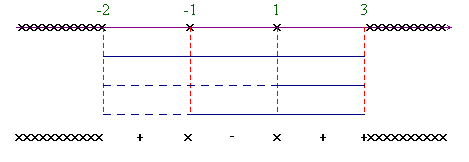
La disequazione è, dunque, verificata
per -2 < x < -1 ![]() 1
< x ≤ 3.
1
< x ≤ 3.