Funzioni trigonometriche
N.B. Tutti gli archi e gli angoli sono misurati esclusivamente in radianti
Premessa
Anche per queste disequazioni, come già per quelle irrazionali e per quelle logaritmiche ed esponenziali, non esistono metodi generali di soluzione e spesso si possono applicare solo metodi numerici, come si può vedere dal seguente esempio.
Esempio. Si debba risolvere la disequazione:
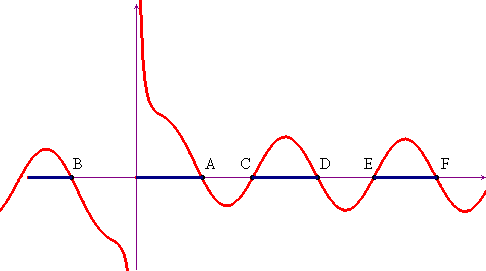
![]() . Si può esaminare la figura seguente
dove abbiamo riportato il grafico della funzione a primo membro
della disequazione. La funzione è dispari (per esempio
xB=-xA), per cui basterà
risolverla per x>0. Si deduce dal grafico che la
disequazione è vera per 0<x<xA
. Si può esaminare la figura seguente
dove abbiamo riportato il grafico della funzione a primo membro
della disequazione. La funzione è dispari (per esempio
xB=-xA), per cui basterà
risolverla per x>0. Si deduce dal grafico che la
disequazione è vera per 0<x<xA
![]() xC<x<xD
xC<x<xD ![]() xE<x<xF, ecc. I valori
xA, xC, xD, ... si
avvicinano sempre di più a multipli di π, in quanto al
crescere di x la quantità 1/x diventa
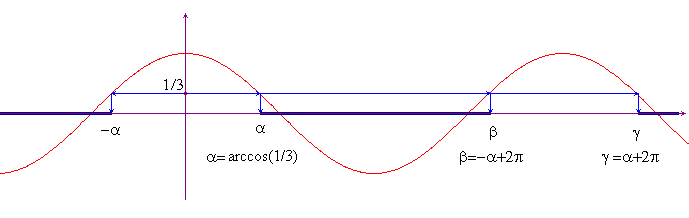
sempre più piccola. Con Cabri si trova:
xA
xE<x<xF, ecc. I valori
xA, xC, xD, ... si
avvicinano sempre di più a multipli di π, in quanto al
crescere di x la quantità 1/x diventa
sempre più piccola. Con Cabri si trova:
xA ![]() 3.42, xC
3.42, xC ![]() 6.11, xD
6.11, xD ![]() 9.53, xE
9.53, xE ![]() 12.47, xF
12.47, xF ![]() 15.79, mentre per π e i suoi multipli si ha π
15.79, mentre per π e i suoi multipli si ha π
![]() 3.14, 2π
3.14, 2π ![]() 6.28, 3π
6.28, 3π ![]() 9.42, 4π
9.42, 4π ![]() 12.56, 5π
12.56, 5π ![]() 15.71.
15.71.
Disequazioni elementari
Sono le disequazioni del tipo:
- sinx > a
- sinx < a
- sinx ≥ a
- sinx ≤ a
- cosx > a
- cosx < a
- cosx ≥ a
- cosx ≤ a
- tanx > a
- tanx < a
- tanx ≥ a
- tanx ≤ a
Abbiamo tralasciato le funzioni cotangente, secante e cosecante, perché di uso meno frequente, ma i metodi indicati si applicano anche ad esse.
Per risolvere disequazioni di questo tipo si possono seguire sostanzialmente due metodi: il primo basato sui grafici delle funzioni in oggetto, il secondo basato sulla definizione delle funzioni trigonometriche e l'uso della circonferenza di centro l'origine e raggio 1. Preferiamo di gran lunga il primo, perché rende più chiaro il problema della periodicità, che è uno dei problemi più importanti connessi con l'uso di questo funzioni. In ogni caso proporremo anche esempi d'uso del secondo metodo. Come al solito ragioneremo su alcuni esempi per chiarire il metodo.
Esempio 1. Risolvere la disequazione ![]() .
.
Uso delle funzioni goniometriche
![]() .
.
Posto Y=sinx e X=cosx, la disequazione data
si può ritenere equivalente al seguente sistema in due
incognite: 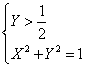 , che è
verificato nell'arco di circonferenza in rosso nel
grafico qui sotto. Tenendo conto della periodicità si
conclude esattamente come sopra:
, che è
verificato nell'arco di circonferenza in rosso nel
grafico qui sotto. Tenendo conto della periodicità si
conclude esattamente come sopra:
![]() .
.
Come già accennato, con questo metodo risulta più difficile leggere la periodicità delle soluzioni.
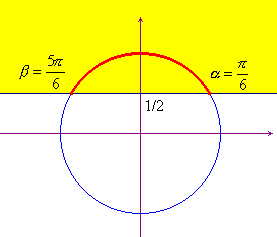
Esempio 2. Risolvere la disequazione ![]() .
.
Uso delle funzioni goniometriche
![]() .
.
Posto Y=sinx e X=cosx, la disequazione data
si può ritenere equivalente al seguente sistema in due
incognite: 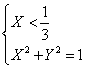 , che è
verificato nell'arco di circonferenza in rosso nel
grafico qui sotto. Tenendo conto della periodicità si
conclude esattamente come sopra:
, che è
verificato nell'arco di circonferenza in rosso nel
grafico qui sotto. Tenendo conto della periodicità si
conclude esattamente come sopra:
![]() .
.
Come già accennato più volte, con questo metodo risulta più difficile leggere la periodicità delle soluzioni.
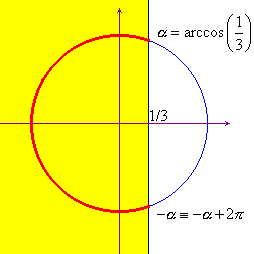
Uso delle funzioni goniometriche
![]() .
.
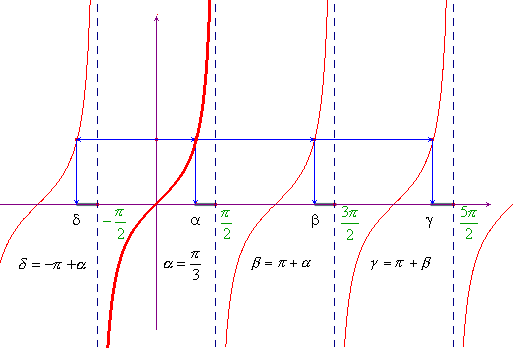
Tracciata la retta di equazione x=1, e riportato il
valore ![]() su di essa, si devono
trovare gli angoli la cui tangente supera
su di essa, si devono
trovare gli angoli la cui tangente supera ![]() . Si tratta degli angoli compresi negli archi segnati
in rosso nel grafico qui sotto. Si traggono naturalmente le
stesse conclusioni di sopra per quanto riguarda le soluzioni:
. Si tratta degli angoli compresi negli archi segnati
in rosso nel grafico qui sotto. Si traggono naturalmente le
stesse conclusioni di sopra per quanto riguarda le soluzioni:
![]() .
.
Nel caso della tangente risulta ancora più facile, con questo metodo, compiere errori sulla periodicità, in quanto la funzione tangente ha una periodicità di mezza circonferenza.
Disequazioni contenenti solo seno, coseno, tangente
Sono le disequazioni del tipo f(sinx) > 0 , o le
analoghe che si ottengono sostituendo il coseno o la tangente al
seno. Si risolvono con la sostituzione sinx=t,
naturalmente a patto che la disequazione f(t) > 0
sia risolubile. Il caso più frequente nelle applicazioni
è quello delle disequazioni di secondo grado in seno,
coseno o tangente: ![]() . Proponiamo un esempio
per chiarire il metodo.
. Proponiamo un esempio
per chiarire il metodo.
Esempio. Risolvere la disequazione ![]() . Posto sinx=t, la disequazione di
secondo grado è verificata per -1<t<1/2.
Si ottiene dunque:
. Posto sinx=t, la disequazione di
secondo grado è verificata per -1<t<1/2.
Si ottiene dunque: 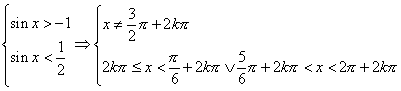 , che porge, come
soluzione finale,
, che porge, come
soluzione finale, ![]() .
.
Disequazioni lineari in seno e coseno
Sono le disequazioni del tipo ![]() .
Si tratta di un tipo di disequazione molto importante nelle
applicazioni. Esistono varie strategie risolutive: ne proporremo
due, segnalando che la prima è quella che ci pare
più semplice. Sconsigliamo l'uso delle cosiddette
formule parametriche (che esprimono il seno e il coseno in
funzione della tangente di x/2).
.
Si tratta di un tipo di disequazione molto importante nelle
applicazioni. Esistono varie strategie risolutive: ne proporremo
due, segnalando che la prima è quella che ci pare
più semplice. Sconsigliamo l'uso delle cosiddette
formule parametriche (che esprimono il seno e il coseno in
funzione della tangente di x/2).
Riduzione ad una disequazione elementare
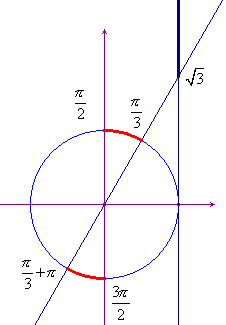
 , esiste sicuramente
un numero α tale che
, esiste sicuramente
un numero α tale che
Esempio. Risolvere la disequazione: ![]() . Seguendo la strategia indicata si
ottiene, successivamente:
. Seguendo la strategia indicata si
ottiene, successivamente: ![]() . Quest'ultima risulta verificata per
. Quest'ultima risulta verificata per ![]() . Le soluzioni cercate sono allora:
. Le soluzioni cercate sono allora: ![]() .
.
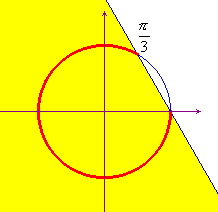
Posto Y=sinx e X=cosx, la disequazione data
si può ritenere equivalente al seguente sistema in due
incognite: ![]() , che si può
risolvere graficamente al solito modo.
, che si può
risolvere graficamente al solito modo.
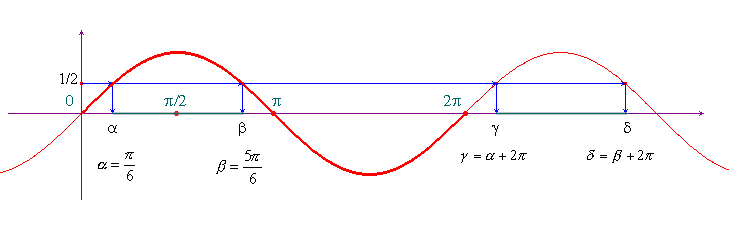
Esempio. Riprendiamo l'esempio di sopra:
![]() . Il sistema diventa:
. Il sistema diventa: 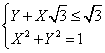 .
.
Il grafico qui sotto mostra subito che l'insieme di
soluzioni è quello già trovato: ![]() .
.
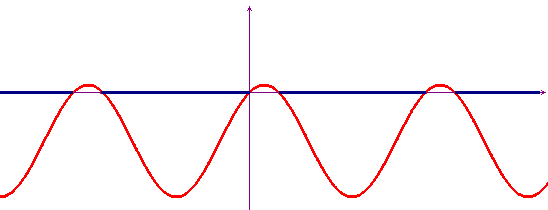
Come al solito, un utile controllo della bontà dei
risultati si ha scrivendo ![]() e tracciando il
grafico della funzione a primo membro. Riportiamo il grafico qui
sotto:
e tracciando il
grafico della funzione a primo membro. Riportiamo il grafico qui
sotto:
 .
.
Disequazioni omogenee di secondo grado in seno e coseno.
Sono le disequazioni del tipo ![]() .
Esse si trasformano in disequazioni lineari con le formule:
.
Esse si trasformano in disequazioni lineari con le formule: ![]() (formule di bisezione e di duplicazione del
seno).
(formule di bisezione e di duplicazione del
seno).
Esempio. Risolvere la disequazione ![]() . Con le formule soprascritte si ottiene:
. Con le formule soprascritte si ottiene: ![]() , che diventa una disequazione lineare con la
posizione 2x=t:
, che diventa una disequazione lineare con la
posizione 2x=t: ![]() . Le sue soluzioni
sono:
. Le sue soluzioni
sono: ![]() . Risostituendo t=2x e,
dopo, dividendo per 2, si ottiene:
. Risostituendo t=2x e,
dopo, dividendo per 2, si ottiene: ![]() .
.
Si presti attenzione a dividere per 2 solo dopo aver
scritto per esteso le soluzioni in t, compresa anche la
periodicità .
Disequazioni simmetriche in seno e coseno
Sono quelle del tipo ![]() , e si chiamano
così perché scambiando il seno con il coseno nulla
cambia. Si riducono a disequazioni di secondo grado in coseno
con la sostituzione
, e si chiamano
così perché scambiando il seno con il coseno nulla
cambia. Si riducono a disequazioni di secondo grado in coseno
con la sostituzione ![]() .
.
Le altre disequazioni
Come già più volte accennato, non esistono tecniche risolutive generali per le disequazioni trigonometriche. Per risolvere quelle che non rientrano nei modelli considerati si devono utilizzare i metodi appresi per le funzioni algebriche, opportunamente adattati. Proponiamo un esempio per chiarire il concetto.
Esempio. Risolvere la disequazione  . Si deve preventivamente trovare il dominio e poi
il segno di ognuno dei fattori. Per ottenere il risultato finale
conviene utilizzare il solito grafico del tipo +/-, con
l'avvertenza che, trattandosi di funzioni periodiche,
è sufficiente considerare un intervallo ampio quanto il
periodo. Tra le operazioni preliminari ci sarà dunque
anche quella di determinare il periodo, cosa non sempre agevole
come mostra il caso della funzione tangente, periodica di
periodo π, ma rapporto di due funzioni di periodo 2π. Nei
casi semplici, trovato il periodo delle singole funzioni,
basterà prendere, se c'è, il minimo comune
multiplo dei periodi. In questo esempio, limitandoci al tratto
tra 0 e 2π, per il dominio bisogna escludere i valori π/4,
3π/4, 7π/4. Riportiamo solo il grafico finale.
. Si deve preventivamente trovare il dominio e poi
il segno di ognuno dei fattori. Per ottenere il risultato finale
conviene utilizzare il solito grafico del tipo +/-, con
l'avvertenza che, trattandosi di funzioni periodiche,
è sufficiente considerare un intervallo ampio quanto il
periodo. Tra le operazioni preliminari ci sarà dunque
anche quella di determinare il periodo, cosa non sempre agevole
come mostra il caso della funzione tangente, periodica di
periodo π, ma rapporto di due funzioni di periodo 2π. Nei
casi semplici, trovato il periodo delle singole funzioni,
basterà prendere, se c'è, il minimo comune
multiplo dei periodi. In questo esempio, limitandoci al tratto
tra 0 e 2π, per il dominio bisogna escludere i valori π/4,
3π/4, 7π/4. Riportiamo solo il grafico finale.
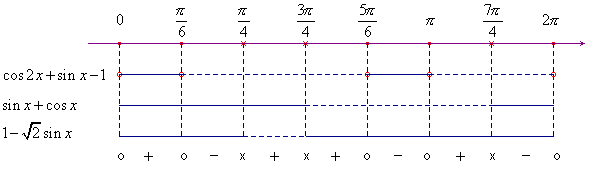
Le soluzioni sono: ![]() .
.
Funzioni trigonometriche inverse
Consigliamo di utilizzare esclusivamente i grafici delle funzioni trigonometriche inverse per risolvere questo tipo di disequazioni. Proponiamo alcuni esempi per chiarire il metodo, limitandoci a casi molto semplici.
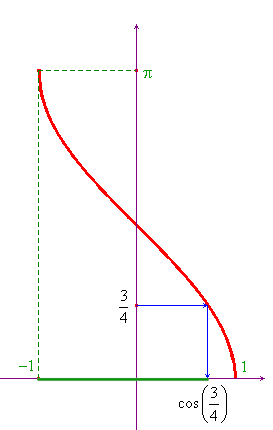
Esempio 1. Risolvere la disequazione ![]() .
.
Tracciato il grafico della funzione f(x)=arcsinx e
riportato il valore π/3 sull'asse delle ordinate, il
grafico di seguito mostra subito che la disequazione è
verificata per ![]() .
.
Per determinare il valore ![]() sull'asse delle
ascisse basta ricordare che la funzione arcseno è
l'inversa, nel tratto tra -π/2 e π/2 della funzione
seno, per cui sull'asse delle ordinate compaiono gli angoli
e sulle delle ascisse i loro seni:
sull'asse delle
ascisse basta ricordare che la funzione arcseno è
l'inversa, nel tratto tra -π/2 e π/2 della funzione
seno, per cui sull'asse delle ordinate compaiono gli angoli
e sulle delle ascisse i loro seni: ![]() .
.
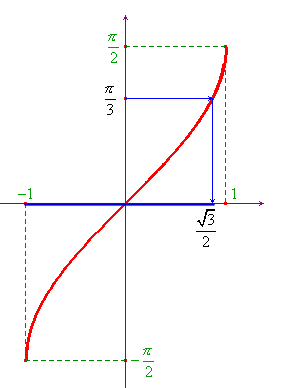
Esempio 2. Risolvere la disequazione ![]() .
.
Esempio 3. Risolvere la disequazione ![]() . Con una sostituzione ormai usuale la
disequazione si riduce a
. Con una sostituzione ormai usuale la
disequazione si riduce a ![]() . La seconda non ha
soluzioni, la prima è verificata per -1 ≤
x < sin1.
. La seconda non ha
soluzioni, la prima è verificata per -1 ≤
x < sin1.