www.batmath.it

Il cuore del problema

Si consideri la funzione f(x)=p₂(x)=x², avente dominio e codominio coincidenti con l'insieme R dei numeri reali.   Essa si può chiamare funzione elevamento al quadrato. Essendo x² positivo per ogni x reale, si deduce subito che la funzione non è suriettiva; poiché poi numeri opposti hanno lo stesso quadrato si conclude immediatamente che la funzione non è nemmeno iniettiva.

Per poterla invertire è dunque indispensabile operare una restrizione sia sul codominio che sul dominio in modo da renderla biunivoca. Mentre la restrizione sul codominio è, per così dire, naturale (nel senso che si tratta di restringere il codominio all'immagine, eliminando dal codominio tutti i "bersagli" che non vengono mai colpiti), non altrettanto succede per la restrizione al dominio. Le possibilità sono molte, e la scelta cade, per motivi di opportunità che appariranno chiari con l'uso, sui reali positivi. Questa restrizione della funzione elevamento al quadrato ai reali positivi, sia sul dominio che sul codominio, produce una funzione biunivoca, e quindi invertibile: la chiameremo, in via provvisoria, π₂(x), per distinguerla dalla funzione p₂(x). Ebbene è proprio l'inversa della funzione π₂(x) che si chiama funzione radice quadrata e si indica con il simbolo o, semplicemente, .

Sulla base delle note proprietà delle funzioni e delle loro inverse si ha subito che , per ogni x reale positivo, e che, analogamente, , sempre per ogni x reale positivo.

Le proprietà della funzione radice quadrata che abbiamo appena definito dipendono in maniera essenziale dalla particolare restrizione che abbiamo voluto considerare per la funzione elevamento al quadrato. In particolare ci interessa qui segnalare che la radice quadrata di un numero reale positivo è sempre un numero positivo(e questo dipende dal fatto che la restrizione sul dominio di p₂(x) è stata fatta prendendo solo i reali positivi).

Naturalmente una volta costruita la funzione radice quadrata, nulla ci impedisce di considerare la sua composta con la funzione elevamento al quadrato, in uno dei due ordini possibili:

cioè le funzioni e . Poiché le due funzioni non sono una l'inversa dell'altra non dovremo affatto meravigliarci del fatto che, in linea di principio, partendo da un certo valore di x e applicando successivamente le due funzioni non si debba necessariamente ritornare allo stesso valore di x (come invece succede quando si applica di seguito una funzione e la sua inversa).

Non è difficile provare che valgono le seguenti uguaglianze:

Per la prima basta osservare che se x è positivo la funzione radice e la funzione p₂ sono una inversa dell'altra (in questo intervallo p₂ e π₂coincidono), se x è negativo si ha x² = (-x)² ed essendo ora -x positivo basta applicare di nuovo quanto appena osservato. Per provare la seconda uguaglianza non sussistono particolari difficoltà, in quanto il primo membro ha senso solo per gli x positivi, intervallo in cui, come già osservato, p₂ e π₂ coincidono. La uguaglianza tra la radice di x² e la funzione valore assoluto può anche essere assunta come definizione di valore assoluto.

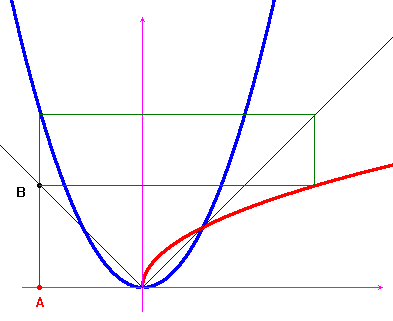
Una verifica intuitiva della proprietà accennata relativa alla funzione  si può fare con la tecnica per la costruzione grafica della funzione composta. Le figure qui sotto provano che, comunque si scelga il punto A, il punto B del grafico della funzione composta sta o sulla bisettrice y=x o su y=-x.

Puoi vedere un'animazione di questa costruzione, con CabriJava.

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 01/12/2000 - ultimo aggiornamento il 01/09/2003